rozwiązanie nierówności w trybie online rozwiązanie prawie każda dana nierówność online. Matematyczny nierówności w internecie rozwiązać matematykę. Znajdź szybko rozwiązanie nierówności w trybie online. Strona www.site pozwala znaleźć rozwiązanie prawie dowolne algebraiczny, trygonometryczny Lub transcendentna nierówność w Internecie. Podczas studiowania prawie każdej gałęzi matematyki na różne etapy muszę zdecydować nierówności w internecie. Aby uzyskać odpowiedź natychmiast, a co najważniejsze, dokładną, potrzebujesz zasobu, który Ci to umożliwi. Dzięki www.site rozwiązać nierówność online zajmie to kilka minut. Główną zaletą www.site przy rozwiązywaniu zadań matematycznych nierówności w internecie- jest szybkość i dokładność udzielonej odpowiedzi. Strona jest w stanie rozwiązać każdy nierówności algebraiczne w Internecie, nierówności trygonometryczne w Internecie, Transcendentalne nierówności w Internecie, I nierówności z nieznanymi parametrami w trybie online. nierówności służyć jako potężny aparat matematyczny rozwiązania zadania praktyczne. Z pomocą nierówności matematyczne możliwe jest wyrażenie faktów i relacji, które na pierwszy rzut oka mogą wydawać się zagmatwane i skomplikowane. nieznane ilości nierówności można znaleźć, formułując problem w matematyczny język w formie nierówności I decydować otrzymane zadanie w trybie online na stronie internetowej www.site. Każdy nierówność algebraiczna, nierówność trygonometryczna Lub nierówności zawierający nadzmysłowy charakteryzuje Cię z łatwością decydować online i uzyskaj właściwą odpowiedź. Studiując nauki przyrodnicze, nieuchronnie napotyka się taką potrzebę rozwiązanie nierówności. W takim przypadku odpowiedź musi być dokładna i musi zostać otrzymana natychmiast w trybie online. Dlatego za rozwiązuj nierówności matematyczne online polecamy stronę www.site, która stanie się Twoim niezastąpionym kalkulatorem rozwiązywać nierówności algebraiczne online, nierówności trygonometryczne w Internecie, I Transcendentalne nierówności w Internecie Lub nierówności o nieznanych parametrach. Do praktycznych problemów znajdowania rozwiązań intravol różnych nierówności matematyczne zasób www.. Rozwiązywanie nierówności w internecie sam, warto sprawdzić otrzymaną odpowiedź za pomocą internetowe rozwiązanie nierówności na stronie internetowej www.site. Konieczne jest prawidłowe zapisanie nierówności i natychmiastowe otrzymanie rozwiązanie internetowe, po czym pozostaje tylko porównać odpowiedź z rozwiązaniem nierówności. Sprawdzenie odpowiedzi zajmie nie więcej niż minutę rozwiązać nierówność online i porównaj odpowiedzi. Pomoże to uniknąć błędów w decyzja i popraw odpowiedź na czas rozwiązywanie nierówności w Internecie albo algebraiczny, trygonometryczny, niedościgniony Lub nierówność o nieznanych parametrach.
Na tej lekcji rozpoczniemy badanie systemów nierówności. Najpierw rozważymy układy nierówności liniowych. Na początku lekcji zastanowimy się, gdzie i dlaczego powstają systemy nierówności. Następnie przestudiujemy, co to znaczy rozwiązać system i zapamiętamy sumę i przecięcie zbiorów. Na koniec rozwiążemy konkretne przykłady układów nierówności liniowych.
Temat: dietanierówności rzeczywiste i ich systemy
Lekcja:Głównykoncepcje, rozwiązywanie układów nierówności liniowych
Do tej pory rozwiązywaliśmy nierówności indywidualne i stosowaliśmy do nich metodę przedziałową, mogły to być nierówności liniowe oraz kwadratowe i racjonalne. Przejdźmy teraz do rozwiązywania układów nierówności - najpierw systemy liniowe. Spójrzmy na przykład, z którego wynika potrzeba uwzględnienia systemów nierówności.
Znajdź zakres funkcji
Znajdź zakres funkcji
Funkcja istnieje, gdy istnieją oba pierwiastki kwadratowe, tj.
![]()
Jak rozwiązać taki system? Należy znaleźć wszystkie x spełniające zarówno pierwszą, jak i drugą nierówności.
Narysuj na osi x zbiór rozwiązań pierwszej i drugiej nierówności.

Naszym rozwiązaniem jest przedział przecięcia dwóch promieni.
Ta metoda przedstawiania rozwiązania układu nierówności nazywana jest czasami metodą dachu.
Rozwiązaniem układu jest przecięcie dwóch zbiorów.
Przedstawmy to graficznie. Mamy zbiór A o arbitralnej naturze i zbiór B o dowolnej naturze, które się przecinają.
Definicja: Przecięciem dwóch zbiorów A i B jest trzeci zbiór, który składa się ze wszystkich elementów zawartych zarówno w A, jak i B.

Rozważ dalej konkretne przykłady rozwiązywanie liniowych układów nierówności, jak znajdować przecięcia zbiorów rozwiązań poszczególnych nierówności wchodzących w skład układu.
Rozwiąż układ nierówności:

Odpowiedź: (7; 10).

4. Rozwiąż układ ![]()
Skąd może wynikać druga nierówność układu? Na przykład z nierówności
Graficznie oznaczamy rozwiązania każdej nierówności i znajdujemy przedział ich przecięcia.

Zatem jeśli mamy układ, w którym jedna z nierówności spełnia dowolną wartość x, to można ją wyeliminować.

Odpowiedź: system jest niespójny.

Rozważaliśmy typowe problemy podporowe, do których sprowadza się rozwiązanie dowolnego liniowego układu nierówności.
Rozważ następujący system.
7. ![]()
![]()

Czasami układ liniowy jest dany przez podwójną nierówność; rozważ ten przypadek.
8. ![]()
![]()
![]()
Zbadaliśmy systemy nierówności liniowych, zrozumieliśmy, skąd się biorą, zbadaliśmy typowe systemy, do których wszyscy doszli systemy liniowe i rozwiązałem niektóre z nich.
1. Mordkovich A.G. i inne Algebra 9. klasa: Proc. Do edukacji ogólnej Instytucje - wyd. 4. - M.: Mnemosyne, 2002.-192 s.: il.
2. Mordkovich A.G. i inne Algebra klasa 9: Zeszyt zadań dla uczniów instytucje edukacyjne/ A. G. Mordkovich, T. N. Miszustina i inni - wyd. 4. — M.: Mnemosyne, 2002.-143 s.: il.
3. Yu N. Makaryczow, Algebra. Klasa 9: podręcznik. dla uczniów szkół ogólnokształcących. instytucje / Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, I. E. Feoktistov. – wydanie 7, wyd. i dodatkowe - M.: Mnemosyne, 2008.
4. Alimov Sh.A., Kolyagin Yu.M., Sidorov Yu.V. Algebra. Stopień 9 16 wyd. - M., 2011. - 287 s.
5. Mordkovich A. G. Algebra. Stopień 9 O 14:00 Część 1. Podręcznik dla uczniów instytucji edukacyjnych / A. G. Mordkovich, P. V. Semenov. - wyd. 12, usunięte. — M.: 2010. — 224 s.: il.
6. Algebra. Stopień 9 Po 2 godzinach Część 2. Zeszyt zadań dla uczniów instytucji edukacyjnych / A. G. Mordkovich, L. A. Aleksandrova, T. N. Miszustina i inni; wyd. A. G. Mordkovich. – wydanie XII, ks. — M.: 2010.-223 s.: il.
1. Portalu Nauki przyrodnicze ().
2. Elektroniczny kompleks edukacyjno-metodyczny do przygotowania klas 10-11 dla egzaminy wstępne z informatyki, matematyki, języka rosyjskiego ().
4. Centrum Edukacyjne „Technologia edukacji” ().
5. Sekcja College.ru poświęcona matematyce ().
1. Mordkovich A.G. i wsp. Algebra klasa 9: Zeszyt zadań dla uczniów instytucji edukacyjnych / A. G. Mordkovich, T. N. Mishustina i wsp. - wyd. 4. - M.: Mnemosyne, 2002.-143 s.: chory. nr 53; 54; 56; 57.
Nierówność to dwie liczby lub wyrażenia matematyczne połączone jednym ze znaków: > (więcej, w przypadku nierówności ścisłych),< (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).
nierówność jest liniowy na takich samych warunkach jak równanie: zawiera zmienne tylko pierwszego stopnia i nie zawiera iloczynów zmiennych.
Rozwiązanie nierówności liniowych i układów nierówności liniowych jest z nimi nierozerwalnie związane zmysł geometryczny: rozwiązaniem nierówności liniowej jest pewna półpłaszczyzna, na którą cała płaszczyzna jest podzielona linią prostą, której równanie jest dane przez nierówność liniową. Na rysunku należy znaleźć tę półpłaszczyznę, a w przypadku układu nierówności liniowych część płaszczyzny ograniczoną kilkoma prostymi.
Do rozwiązania układów nierówności liniowych z duża liczba zmienne redukują wiele problemów ekonomicznych, w szczególności problemów programowania liniowego, w których wymagane jest znalezienie maksimum lub minimum funkcji.
Rozwiązywanie układów nierówności liniowych z dowolną liczbą niewiadomych
Przeanalizujmy najpierw nierówności liniowe na płaszczyźnie. Rozważmy jedną nierówność z dwiema zmiennymi i:
![]() ,
,
gdzie są współczynniki zmiennych (niektóre liczby), jest terminem wolnym (także pewną liczbą).
Jedna nierówność z dwiema niewiadomymi, podobnie jak równanie, ma nieskończoną liczbę rozwiązań. Rozwiązaniem tej nierówności jest para liczb spełniających tę nierówność. Geometrycznie zbiór rozwiązań nierówności przedstawia się jako półpłaszczyznę ograniczoną linią prostą
![]() ,
,
którą nazwiemy linią graniczną.
Krok 1. Skonstruuj prostą ograniczającą zbiór rozwiązań nierówności liniowej
Aby to zrobić, musisz znać dowolne dwa punkty tej linii. Znajdźmy punkty przecięcia z osiami współrzędnych. Współrzędna przecięcia A wynosi zero (rysunek 1). Wartości liczbowe na osiach na tym rysunku odnoszą się do przykładu 1, który przeanalizujemy zaraz po tej teoretycznej dygresji.

Odciętą znajdujemy rozwiązując układowo równanie prostej z równaniem osi.
Znajdźmy przecięcie z osią:
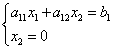
Podstawiając wartość do pierwszego równania, otrzymujemy
Gdzie .
W ten sposób znaleźliśmy odciętą punktu A .
Znajdźmy współrzędne punktu przecięcia z osią.
Punkt odciętej B równa się zeru. Rozwiążmy równanie linii granicznej za pomocą równania osi współrzędnych:

![]() ,
,
stąd współrzędne punktu B: .
Krok 2. Narysuj linię ograniczającą zbiór rozwiązań do nierówności. Znajomość punktów A I B przecięcia linii granicznej z osiami współrzędnych, możemy narysować tę linię. Linia prosta (znowu rysunek 1) dzieli całą płaszczyznę na dwie części leżące po prawej i lewej stronie (powyżej i poniżej) tej prostej.
Krok 3. Ustal, która z półpłaszczyzn jest rozwiązaniem tej nierówności. Aby to zrobić, musimy podstawić początek współrzędnych (0; 0) do tej nierówności. Jeżeli współrzędne początku spełniają nierówność, to rozwiązaniem nierówności jest półpłaszczyzna, w której znajduje się początek. Jeżeli współrzędne nie spełniają nierówności, wówczas rozwiązaniem nierówności jest półpłaszczyzna niezawierająca początku. Półpłaszczyzna rozwiązania nierówności będzie oznaczona kreskami z prostej wewnątrz półpłaszczyzny, jak na rysunku 1.
Jeśli rozwiążemy układ nierówności liniowych, wówczas każdy krok jest wykonywany dla każdej nierówności układu.
Przykład 1 Rozwiąż nierówność
Rozwiązanie. Narysujmy linię prostą
Podstawiając linię prostą do równania otrzymujemy i podstawiając otrzymujemy. Dlatego będą współrzędne punktów przecięcia z osiami A(3; 0) , B(0; 2) . Narysuj linię prostą przechodzącą przez te punkty (ponownie, rysunek 1).

Wybieramy półpłaszczyznę rozwiązań nierówności. W tym celu podstawiamy współrzędne początku (0; 0) do nierówności:
otrzymujemy , tj. współrzędne początku spełniają tę nierówność. W konsekwencji rozwiązaniem nierówności jest półpłaszczyzna zawierająca początek, czyli lewa (lub dolna) półpłaszczyzna.
Gdyby ta nierówność była ścisła, to znaczy miałaby postać
wówczas punkty linii granicznej nie byłyby rozwiązaniem, gdyż nie spełniają nierówności.
Rozważmy teraz układ nierówności liniowych z dwiema niewiadomymi:
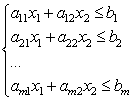
Każda z nierówności tego układu na płaszczyźnie definiuje półpłaszczyznę. Układ nierówności liniowych nazywa się spójnym, jeśli ma co najmniej jedno rozwiązanie, a niespójnym, jeśli nie ma rozwiązań. Rozwiązaniem układu nierówności liniowych jest dowolna para liczb (), która spełnia wszystkie nierówności tego układu.
Geometrycznie rozwiązaniem układu nierówności liniowych jest zbiór punktów spełniających wszystkie nierówności układu, czyli część wspólna powstałych półpłaszczyzn. Dlatego geometrycznie, w ogólnym przypadku, rozwiązanie można przedstawić jako pewien wielokąt, w konkretnym przypadku może to być linia, odcinek, a nawet punkt. Jeśli układ nierówności liniowych jest niespójny, to nie ma na płaszczyźnie ani jednego punktu spełniającego wszystkie nierówności układu.
Przykład 2
Rozwiązanie. Należy więc znaleźć wielokąt rozwiązań tego układu nierówności. Konstruujemy linię graniczną dla pierwszej nierówności, czyli linię, oraz linię graniczną dla drugiej nierówności, czyli linię.
Robimy to krok po kroku, jak pokazano w odnośniku teoretycznym oraz w przykładzie 1, tym bardziej, że w przykładzie 1 zbudowano linię graniczną dla nierówności, która jest pierwszą w tym układzie.

Półpłaszczyzny rozwiązania odpowiadające nierównościom tego układu są zacieniowane do wewnątrz na rysunku 2. Wspólną częścią półpłaszczyzn rozwiązania jest kąt otwarty ABC. Oznacza to, że zbiór punktów na płaszczyźnie tworzących kąt otwarty ABC, jest rozwiązaniem zarówno pierwszej, jak i drugiej nierówności układu, czyli jest rozwiązaniem układu dwóch nierówności liniowych. Inaczej mówiąc, współrzędne dowolnego punktu z tego zbioru spełniają obie nierówności układu.
Przykład 3 Rozwiązać układ nierówności liniowych
Rozwiązanie. Skonstruujmy linie graniczne odpowiadające nierównościom układu. Robimy to postępując zgodnie z krokami podanymi w tle teoretycznym dla każdej nierówności. Teraz definiujemy półpłaszczyznę rozwiązań każdej nierówności (rysunek 3).

Półpłaszczyzny rozwiązania odpowiadające nierównościom danego układu są zacienione do wewnątrz. Przecięcie półpłaszczyzn rozwiązań przedstawiono, jak pokazano na rysunku, w postaci czworoboku ABCE. Stwierdziliśmy, że wielokątem rozwiązania układu nierówności liniowych z dwiema zmiennymi jest czworokąt ABCE .
Wszystko, co opisano powyżej na temat układów nierówności liniowych z dwiema niewiadomymi, odnosi się również do układu nierówności z dowolną liczbą niewiadomych, z tą tylko różnicą, że rozwiązanie nierówności z N nieznane będzie całością N liczby () spełniające wszystkie nierówności, a zamiast linii granicznej powstanie hiperpłaszczyzna graniczna N-przestrzeń wymiarowa. Rozwiązaniem będzie wielościan rozwiązania (simpleks) ograniczony hiperpłaszczyznami.
System nierówności.
Przykład 1. Znajdź zakres wyrażenia
Rozwiązanie. pod znakiem pierwiastek kwadratowy musi być liczba nieujemna, co oznacza, że dwie nierówności muszą jednocześnie zachodzić: ![]() Mówi się, że w takich przypadkach problem sprowadza się do rozwiązania układu nierówności
Mówi się, że w takich przypadkach problem sprowadza się do rozwiązania układu nierówności
Ale z takim modelem matematycznym (systemem nierówności) jeszcze się nie spotkaliśmy. Oznacza to, że nie jesteśmy jeszcze w stanie ukończyć rozwiązania przykładu.
Nierówności tworzące układ łączymy nawiasem klamrowym (podobnie jest w przypadku układów równań). Na przykład wpis

oznacza, że nierówności 2x - 1 > 3 i 3x - 2< 11 образуют систему неравенств.
Czasami układ nierówności zapisuje się jako nierówność podwójną. Na przykład system nierówności
można zapisać jako podwójną nierówność 3<2х-1<11.
Na kursie algebry w klasie 9 będziemy rozważać jedynie układy dwóch nierówności.
Rozważmy system nierówności

Możesz wybrać kilka jego konkretnych rozwiązań, na przykład x = 3, x = 4, x = 3,5. Rzeczywiście dla x = 3 pierwsza nierówność przyjmuje postać 5 > 3, a druga postać 7< 11. Получились два верных числовых неравенства, значит, х = 3 - решение системы неравенств. Точно так же можно убедиться в том, что х = 4, х = 3,5 - решения системы неравенств.
Jednocześnie wartość x = 5 nie jest rozwiązaniem układu nierówności. Dla x = 5 pierwsza nierówność przyjmuje postać 9 > 3 - poprawną nierówność liczbową, a druga - postać 13< 11- неверное числовое неравенство .
Rozwiązanie układu nierówności oznacza znalezienie wszystkich jego konkretnych rozwiązań. Jest oczywiste, że takie zgadywanie, jak pokazano powyżej, nie jest metodą rozwiązywania układu nierówności. W poniższym przykładzie pokażemy, jak zwykle argumentuje się, rozwiązując system nierówności.
Przykład 3 Rozwiąż układ nierówności:
Rozwiązanie.
A) Rozwiązując pierwszą nierówność układu, znajdujemy 2x > 4, x > 2; rozwiązując drugą nierówność układu, znajdujemy Zx< 13 Отметим эти промежутки на одной координатной прямой , использовав для выделения первого промежутка верхнюю штриховку, а для второго - нижнюю штриховку (рис. 22). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. В рассматриваемом примере получаем интервал
B) Rozwiązując pierwszą nierówność układu, znajdujemy x > 2; znajdujemy rozwiązanie drugiej nierówności układu ![]() Luki te zaznaczamy na jednej linii współrzędnych, stosując kreskowanie górne dla pierwszej szczeliny, a kreskowanie dolne dla drugiej (ryc. 23). Rozwiązaniem układu nierówności będzie przecięcie rozwiązań nierówności układu, tj. odstęp, w którym oba kreskowania pokrywają się. W rozważanym przykładzie otrzymujemy belkę
Luki te zaznaczamy na jednej linii współrzędnych, stosując kreskowanie górne dla pierwszej szczeliny, a kreskowanie dolne dla drugiej (ryc. 23). Rozwiązaniem układu nierówności będzie przecięcie rozwiązań nierówności układu, tj. odstęp, w którym oba kreskowania pokrywają się. W rozważanym przykładzie otrzymujemy belkę

V) Rozwiązując pierwszą nierówność układu, znajdujemy x< 2; решая второе неравенство системы, находим Отметим эти промежутки на одной координатной прямой, использовав для первого промежутка верхнюю штриховку, а для второго - нижнюю штриховку (рис. 24). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. Здесь такого промежутка нет, значит, система неравенств не имеет решений.

Uogólnijmy rozumowanie przeprowadzone w rozpatrywanym przykładzie. Załóżmy, że musimy rozwiązać układ nierówności

Niech np. przedział (a, b) będzie rozwiązaniem nierówności fx 2 > g (x), a przedział (c, d) będzie rozwiązaniem nierówności f 2 (x) > s 2 (x ). Luki te zaznaczamy na jednej linii współrzędnych, stosując kreskowanie górne dla pierwszej szczeliny, a kreskowanie dolne dla drugiej (ryc. 25). Rozwiązaniem układu nierówności jest przecięcie rozwiązań nierówności układu, tj. odstęp, w którym oba kreskowania pokrywają się. Na ryc. 25 to przedział (s, b).

Teraz możemy łatwo rozwiązać układ nierówności, który otrzymaliśmy powyżej, w przykładzie 1:
Rozwiązując pierwszą nierówność układu, znajdujemy x > 2; rozwiązując drugą nierówność układu, znajdujemy x< 8. Отметим эти промежутки (лучи) на одной координатной прямой, использовав для первого -верхнюю, а для второго - нижнюю штриховку (рис. 26). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали, - отрезок . Это - область определения того выражения, о котором шла речь в примере 1.

Oczywiście układ nierówności nie musi składać się z nierówności liniowych, jak to miało miejsce dotychczas; mogą wystąpić wszelkie racjonalne (i nie tylko racjonalne) nierówności. Technicznie rzecz biorąc, praca z systemem racjonalnych nierówności nieliniowych jest oczywiście trudniejsza, ale nie jest to nic zasadniczo nowego (w porównaniu z systemami nierówności liniowych).
Przykład 4 Rozwiązać układ nierówności
Rozwiązanie.
1) Rozwiąż nierówność, którą mamy ![]()
Zwróć uwagę na punkty -3 i 3 na osi liczbowej (ryc. 27). Dzielą prostą na trzy przedziały i na każdym przedziale wyrażenie p(x) = (x - 3)(x + 3) zachowuje znak stały - znaki te pokazano na ryc. 27. Interesują nas przedziały, w których spełniona jest nierówność p(x) > 0 (zacieniowano je na rys. 27) oraz punkty, w których spełniona jest równość p(x) = 0, tj. punkty x \u003d -3, x \u003d 3 (zaznaczono je na ryc. 2 7 ciemnymi kółkami). Zatem na rys. 27 pokazuje model geometryczny rozwiązania pierwszej nierówności.

2) Rozwiąż nierówność, którą mamy
Zwróć uwagę na punkty 0 i 5 na osi liczbowej (ryc. 28). Dzielą linię na trzy przedziały i na każdym z nich wyrażenie<7(х) = х(5 - х) сохраняет постоянный знак - эти знаки указаны на рис. 28. Нас интересуют промежутки, на которых выполняется неравенство g(х) >O (zacieniony na ryc. 28) oraz punkty, w których spełniona jest równość g (x) - O, tj. punkty x = 0, x = 5 (zaznaczono je na ryc. 28 ciemnymi kółkami). Zatem na rys. 28 przedstawia model geometryczny rozwiązania drugiej nierówności układu.

3)
Znalezione rozwiązania pierwszej i drugiej nierówności układu zaznaczamy na jednej linii współrzędnych, stosując górne kreskowanie dla rozwiązań pierwszej nierówności, a dolne kreskowanie dla rozwiązań drugiej nierówności (rys. 29). Rozwiązaniem układu nierówności będzie przecięcie rozwiązań nierówności układu, tj. odstęp, w którym oba kreskowania pokrywają się. Taki przedział jest segmentem.

Przykład 5 Rozwiąż układ nierówności:

Rozwiązanie:
A) Z pierwszej nierówności znajdujemy x >2. Rozważmy drugą nierówność. Trójmian kwadratowy x 2 + x + 2 nie ma pierwiastków rzeczywistych, a jego współczynnik wiodący (współczynnik przy x 2) jest dodatni. Oznacza to, że dla każdego x nierówność x 2 + x + 2>0 jest spełniona, a zatem druga nierówność układu nie ma rozwiązań. Co to oznacza dla systemu nierówności? Oznacza to, że układ nie ma rozwiązań.
B) Z pierwszej nierówności znajdujemy x > 2, a druga nierówność dotyczy dowolnych wartości x. Co to oznacza dla systemu nierówności? Oznacza to, że jego rozwiązanie ma postać x>2, tj. pokrywa się z rozwiązaniem pierwszej nierówności.
Odpowiedź:
a) nie ma żadnych decyzji; B) x>2.
Ten przykład jest ilustracją następujących przydatnych informacji
1. Jeżeli w układzie kilku nierówności z jedną zmienną jedna nierówność nie ma rozwiązań, to układ nie ma rozwiązań.
2. Jeżeli w układzie dwóch nierówności z jedną zmienną jest spełniona jedna nierówność dla dowolnych wartości zmiennej, to rozwiązaniem układu jest rozwiązanie drugiej nierówności układu.
Kończąc tę sekcję, wróćmy do problemu liczby wymyślonej podanej na początku i rozwiążmy ją, jak to mówią, zgodnie ze wszystkimi regułami.
Przykład 2(patrz s. 29). Poczęty Liczba naturalna. Wiadomo, że jeśli do kwadratu liczby pojmowanej dodamy 13, to suma będzie większa od iloczynu liczby poczętej i liczby 14. Jeżeli do kwadratu liczby poczętej dodamy 45, wówczas suma wyniesie Być mniej produktu liczba wymyślona i liczba 18. Jaka liczba została wymyślona?
Rozwiązanie.
Pierwszy etap. Opracowanie modelu matematycznego.
Zamierzona liczba x, jak widzieliśmy powyżej, musi spełniać system nierówności
![]()
Druga faza. Pracując ze skompilowanym modelem matematycznym, przekształćmy pierwszą nierówność układu do postaci
x2- 14x+ 13 > 0.
Znajdźmy pierwiastki trójmianu x 2 - 14x + 13: x 2 \u003d 1, x 2 \u003d 13. Korzystając z paraboli y \u003d x 2 - 14x + 13 (ryc. 30), dochodzimy do wniosku, że nierówność interesujące nas jest spełnione dla x< 1 или x > 13.
Przekształćmy drugą nierówność układu do postaci x2 - 18 2 + 45< 0. Найдем корни трехчлена х 2 - 18x + 45: = 3, х 2 = 15.
Spójrzmy na przykłady rozwiązywania układu nierówności liniowych.
4x + 29 \end(array) \right.\]" title="Wyrenderowane przez QuickLaTeX.com">!}
Aby rozwiązać system, potrzebna jest każda z jego nierówności składowych. Podjęto dopiero decyzję o zapisaniu nie osobno, ale razem, łącząc je nawiasem klamrowym.
W każdej nierówności układu niewiadome przenosimy na jedną stronę, znane na drugą z przeciwnym znakiem:
Title="Wyrenderowane przez QuickLaTeX.com">!}
Po uproszczeniu obie części nierówności należy podzielić przez liczbę przed x. Pierwszą nierówność dzielimy przez liczbę dodatnią, więc znak nierówności się nie zmienia. Drugą nierówność dzielimy przez liczbę ujemną, zatem znak nierówności należy odwrócić:
Title="Wyrenderowane przez QuickLaTeX.com">!}
Rozwiązanie nierówności zaznaczamy na osiach liczbowych:

W odpowiedzi zapisujemy przecięcie rozwiązań, czyli część, w której cieniowanie znajduje się na obu liniach.
Odpowiedź: x∈[-2;1).
Pozbądźmy się ułamka z pierwszej nierówności. Aby to zrobić, mnożymy obie części wyraz po wyrazie przez najmniejszy wspólny mianownik 2. Po pomnożeniu przez liczbę dodatnią znak nierówności nie zmienia się.
Otwórz nawiasy w drugiej nierówności. Iloczyn sumy i różnicy dwóch wyrażeń jest równy różnicy kwadratów tych wyrażeń. Po prawej stronie znajduje się kwadrat różnicy między tymi dwoma wyrażeniami.
Title="Wyrenderowane przez QuickLaTeX.com">!}
Niewiadome przenosimy na jedną stronę, znane na drugą z przeciwnym znakiem i upraszczamy:
![]()
![]()
Podziel obie strony nierówności przez liczbę przed x. W pierwszej nierówności dzielimy przez liczbę ujemną, więc znak nierówności zostaje odwrócony. W drugim dzielimy przez liczbę dodatnią, znak nierówności się nie zmienia:
Title="Wyrenderowane przez QuickLaTeX.com">!}
Obie nierówności oznaczono jako „mniejsze niż” (nie jest istotne, aby jeden znak był ściśle „mniejszy niż”, drugi nie był ścisły, „mniejszy lub równy”). Nie możemy zaznaczyć obu rozwiązań, ale zastosować regułę „”. Najmniejsza liczba wynosi 1, zatem system sprowadza się do nierówności
Zaznaczamy jego rozwiązanie na osi liczbowej:
![]()
Odpowiedź: x∈(-∞;1].
Otwieramy nawiasy. W pierwszej nierówności - . Jest równa sumie sześcianów tych wyrażeń.
W drugim - iloczyn sumy i różnicy dwóch wyrażeń, który jest równy różnicy kwadratów. Ponieważ przed nawiasami znajduje się znak minus, lepiej otworzyć je w dwóch etapach: najpierw użyj formuły, a dopiero potem otwórz nawiasy, zmieniając znak każdego terminu na przeciwny.
![]()
![]()
Niewiadome przenosimy na jedną stronę, znane na drugą z przeciwnym znakiem:
![]()
![]()
Title="Wyrenderowane przez QuickLaTeX.com">!}
Obydwa są większe niż znaki. Stosując zasadę „więcej niż więcej” redukujemy układ nierówności do jednej nierówności. Większa z tych dwóch liczb to 5, więc
Title="Wyrenderowane przez QuickLaTeX.com">!}
Zaznaczamy rozwiązanie nierówności na osi liczbowej i zapisujemy odpowiedź: ![]()
Odpowiedź: x∈(5;∞).
Ponieważ układy nierówności liniowych występują w algebrze nie tylko jako samodzielne zadania, ale także w trakcie rozwiązywania różnego rodzaju równań, nierówności itp., ważne jest, aby z czasem poznać ten temat.
Następnym razem rozważymy przykłady rozwiązywania układów nierówności liniowych w szczególnych przypadkach, gdy jedna z nierówności nie ma rozwiązań lub jej rozwiązaniem jest dowolna liczba.
Rubryka: |

