มุมระหว่างเวกเตอร์
เพื่อให้เราแนะนำแนวคิดเกี่ยวกับผลคูณเวกเตอร์ของเวกเตอร์สองตัว เราต้องเข้าใจแนวคิดดังกล่าวก่อนว่ามุมระหว่างเวกเตอร์เหล่านี้
ให้เราได้รับเวกเตอร์สองตัว $\overline(α)$ และ $\overline(β)$ ลองหาจุด $O$ ในอวกาศแล้วพล็อตเวกเตอร์ $\overline(α)=\overline(OA)$ และ $\overline(β)=\overline(OB)$ จากนั้นจึงทำมุม $AOB$ จะถูกเรียกว่ามุมระหว่างเวกเตอร์เหล่านี้ (รูปที่ 1)
สัญลักษณ์: $∠(\overline(α),\overline(β))$
แนวคิดเกี่ยวกับผลคูณเวกเตอร์ของเวกเตอร์และสูตรในการค้นหา
คำจำกัดความ 1
ผลคูณเวกเตอร์ของเวกเตอร์สองตัวคือเวกเตอร์ที่ตั้งฉากกับเวกเตอร์ทั้งสองที่กำหนด และความยาวของมันจะเท่ากับผลคูณของความยาวของเวกเตอร์เหล่านี้ด้วยไซน์ของมุมระหว่างเวกเตอร์เหล่านี้ และเวกเตอร์นี้ที่มีเวกเตอร์เริ่มต้นสองตัวก็มี การวางแนวเดียวกับระบบพิกัดคาร์ทีเซียน
สัญกรณ์: $\overline(α)х\overline(β)$.
ในทางคณิตศาสตร์ดูเหมือนว่านี้:
- $|\overline(α)х\overline(β)|=|\overline(α)||\overline(β)|sin∠(\overline(α),\overline(β))$
- $\overline(α)х\overline(β)⊥\overline(α)$, $\overline(α)х\overline(β)⊥\overline(β)$
- $(\overline(α)х\overline(β),\overline(α),\overline(β))$ และ $(\overline(i),\overline(j),\overline(k))$ คือ มุ่งเน้นเดียวกัน (รูปที่ 2)
แน่นอนว่าผลคูณภายนอกของเวกเตอร์จะเท่ากับเวกเตอร์ศูนย์ในสองกรณี:
- ถ้าความยาวของเวกเตอร์ตัวใดตัวหนึ่งหรือทั้งสองตัวเป็นศูนย์
- ถ้ามุมระหว่างเวกเตอร์เหล่านี้เท่ากับ $180^\circ$ หรือ $0^\circ$ (เนื่องจากในกรณีนี้ ไซน์เป็นศูนย์)
หากต้องการดูอย่างชัดเจนว่าผลิตภัณฑ์เวกเตอร์ของเวกเตอร์ถูกค้นพบได้อย่างไร ให้พิจารณาตัวอย่างการแก้ปัญหาต่อไปนี้
ตัวอย่างที่ 1
ค้นหาความยาวของเวกเตอร์ $\overline(δ)$ ซึ่งจะเป็นผลคูณเวกเตอร์ของเวกเตอร์ โดยมีพิกัด $\overline(α)=(0,4,0)$ และ $\overline(β) =(3,0,0 )$.
สารละลาย.
ลองพรรณนาเวกเตอร์เหล่านี้ในพื้นที่พิกัดคาร์ทีเซียน (รูปที่ 3):
รูปที่ 3 เวกเตอร์ในปริภูมิพิกัดคาร์ทีเซียน Author24 - แลกเปลี่ยนผลงานนักศึกษาออนไลน์
เราจะเห็นว่าเวกเตอร์เหล่านี้อยู่บนแกน $Ox$ และ $Oy$ ตามลำดับ ดังนั้น มุมระหว่างพวกมันจะเท่ากับ $90^\circ$ ลองหาความยาวของเวกเตอร์เหล่านี้:
$|\โอเวอร์ไลน์(α)|=\sqrt(0+16+0)=4$
$|\overline(β)|=\sqrt(9+0+0)=3$
จากนั้น ตามคำจำกัดความ 1 เราได้รับโมดูล $|\overline(δ)|$
$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$
คำตอบ: $12$.
การคำนวณผลคูณไขว้จากพิกัดเวกเตอร์
คำจำกัดความ 1 หมายถึงวิธีการค้นหาผลคูณเวกเตอร์ของเวกเตอร์สองตัวทันที เนื่องจากเวกเตอร์ นอกจากค่าของมันแล้ว ยังมีทิศทางด้วย จึงเป็นไปไม่ได้ที่จะค้นหาโดยใช้ปริมาณสเกลาร์เท่านั้น แต่นอกเหนือจากนี้ ยังมีวิธีหาเวกเตอร์ที่กำหนดให้เราโดยใช้พิกัดอีกด้วย
ให้เวกเตอร์ $\overline(α)$ และ $\overline(β)$ ซึ่งจะมีพิกัด $(α_1,α_2,α_3)$ และ $(β_1,β_2,β_3)$ ตามลำดับ จากนั้นสามารถหาเวกเตอร์ของผลคูณไขว้ (นั่นคือพิกัด) ได้โดยใช้สูตรต่อไปนี้:
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$
มิฉะนั้น เมื่อขยายดีเทอร์มิแนนต์ เราจะได้พิกัดต่อไปนี้
$\overline(α)х\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$
ตัวอย่างที่ 2
ค้นหาเวกเตอร์ของผลิตภัณฑ์เวกเตอร์ของเวกเตอร์คอลลิเนียร์ $\overline(α)$ และ $\overline(β)$ ด้วยพิกัด $(0,3,3)$ และ $(-1,2,6)$
สารละลาย.
ลองใช้สูตรที่ให้ไว้ข้างต้น เราได้รับ
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18 -6)\overline(i)-(0+3)\overline(j)+(0+3)\overline(k)=12\overline(i)-3\overline(j)+3\overline(k) )=(12,-3,3)$
คำตอบ: $(12,-3,3)$.
คุณสมบัติของผลิตภัณฑ์เวกเตอร์ของเวกเตอร์
สำหรับเวกเตอร์สามตัวที่ผสมกันตามอำเภอใจ $\overline(α)$, $\overline(β)$ และ $\overline(γ)$ เช่นเดียวกับ $r∈R$ จะมีคุณสมบัติต่อไปนี้:
ตัวอย่างที่ 3
ค้นหาพื้นที่ของสี่เหลี่ยมด้านขนานที่จุดยอดมีพิกัด $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ และ $(3,8,0) $.
สารละลาย.
ก่อนอื่น เรามาพรรณนารูปสี่เหลี่ยมด้านขนานนี้ในพื้นที่พิกัด (รูปที่ 5):
รูปที่ 5 สี่เหลี่ยมด้านขนานในพื้นที่พิกัด Author24 - แลกเปลี่ยนผลงานนักศึกษาออนไลน์
เราจะเห็นว่าด้านทั้งสองของสี่เหลี่ยมด้านขนานนี้ถูกสร้างขึ้นโดยใช้เวกเตอร์คอลลิเนียร์ที่มีพิกัด $\overline(α)=(3,0,0)$ และ $\overline(β)=(0,8,0)$ เมื่อใช้คุณสมบัติที่สี่เราได้รับ:
$S=|\overline(α)х\overline(β)|$
ลองหาเวกเตอร์ $\overline(α)х\overline(β)$:
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline (i)-0\overline(j)+24\overline(k)=(0,0,24)$
เพราะฉะนั้น
$S=|\overline(α)х\overline(β)|=\sqrt(0+0+24^2)=24$
ในบทนี้ เราจะดูการดำเนินการกับเวกเตอร์อีกสองรายการ: ผลคูณเวกเตอร์ของเวกเตอร์และ ผลคูณผสมของเวกเตอร์ (ลิงค์ทันทีสำหรับผู้ที่ต้องการมัน). ไม่เป็นไร บางครั้งมันก็เกิดขึ้นเพื่อความสุขที่สมบูรณ์นอกเหนือจากนั้น ผลคูณสเกลาร์ของเวกเตอร์จำเป็นต้องมีมากขึ้นเรื่อยๆ นี่คือการเสพติดเวกเตอร์ อาจดูเหมือนว่าเรากำลังเข้าสู่ป่าแห่งเรขาคณิตเชิงวิเคราะห์ นี่เป็นสิ่งที่ผิด ในคณิตศาสตร์ชั้นสูงส่วนนี้ โดยทั่วไปแล้วจะมีไม้เพียงเล็กน้อย ยกเว้นบางทีอาจจะเพียงพอสำหรับพินอคคิโอ ในความเป็นจริงวัสดุนี้เป็นเรื่องธรรมดาและเรียบง่าย - แทบจะไม่ซับซ้อนไปกว่านี้อีกแล้ว ผลิตภัณฑ์สเกลาร์จะมีงานทั่วไปน้อยลงด้วยซ้ำ สิ่งสำคัญในเรขาคณิตเชิงวิเคราะห์ อย่างที่หลายคนเชื่อหรือเชื่ออยู่แล้ว ไม่ใช่การทำผิดพลาดในการคำนวณ ทำซ้ำเหมือนมนต์สะกดแล้วคุณจะมีความสุข =)
หากเวกเตอร์ส่องแสงอยู่ที่ไหนสักแห่งที่อยู่ห่างไกล เช่น ฟ้าแลบบนขอบฟ้า ก็ไม่สำคัญ ให้เริ่มด้วยบทเรียน เวกเตอร์สำหรับหุ่นจำลองเพื่อฟื้นฟูหรือรับความรู้พื้นฐานเกี่ยวกับเวกเตอร์ ผู้อ่านที่เตรียมพร้อมมากขึ้นสามารถทำความคุ้นเคยกับข้อมูลแบบเลือกได้ฉันพยายามรวบรวมตัวอย่างที่สมบูรณ์ที่สุดที่มักพบในทางปฏิบัติ
อะไรจะทำให้คุณมีความสุขทันที? เมื่อตอนที่ฉันยังเด็ก ฉันสามารถเล่นปาหี่ลูกบอลสองหรือสามลูกได้ มันได้ผลดี ตอนนี้คุณไม่จำเป็นต้องเล่นปาหี่เลยเพราะเราจะพิจารณา เวกเตอร์เชิงพื้นที่เท่านั้นและเวกเตอร์แฟลตที่มีพิกัดสองพิกัดจะถูกละไว้ ทำไม นี่คือที่มาของการกระทำเหล่านี้ - เวกเตอร์และผลคูณผสมของเวกเตอร์ถูกกำหนดและทำงานในพื้นที่สามมิติ ง่ายกว่านี้แล้ว!
การดำเนินการนี้เกี่ยวข้องกับผลคูณสเกลาร์ด้วย เวกเตอร์สองตัว. ปล่อยให้สิ่งเหล่านี้เป็นตัวอักษรที่ไม่เน่าเปื่อย
การกระทำนั้นเอง แสดงโดยดังต่อไปนี้: . มีตัวเลือกอื่นๆ แต่ฉันคุ้นเคยกับการแทนผลคูณเวกเตอร์ของเวกเตอร์ด้วยวิธีนี้ในวงเล็บเหลี่ยมที่มีเครื่องหมายกากบาท
และทันที คำถาม: ถ้าเข้า. ผลคูณสเกลาร์ของเวกเตอร์เวกเตอร์สองตัวเกี่ยวข้องกัน และตรงนี้เวกเตอร์สองตัวก็คูณด้วย อะไรคือความแตกต่าง? ความแตกต่างที่ชัดเจนประการแรกคือในผลลัพธ์:
ผลลัพธ์ของผลิตภัณฑ์สเกลาร์ของเวกเตอร์คือ NUMBER:
ผลลัพธ์ของผลคูณไขว้ของเวกเตอร์คือ VECTOR: นั่นคือเราคูณเวกเตอร์แล้วได้เวกเตอร์อีกครั้ง สโมสรปิด. ที่จริงแล้วนี่คือที่มาของชื่อของการดำเนินการ ในวรรณกรรมด้านการศึกษาที่แตกต่างกัน การกำหนดอาจแตกต่างกัน ฉันจะใช้ตัวอักษร
คำจำกัดความของผลิตภัณฑ์ข้าม
อันดับแรกจะมีคำจำกัดความพร้อมรูปภาพแล้วแสดงความคิดเห็น
คำนิยาม: สินค้าเวกเตอร์ ไม่ใช่คอลลิเนียร์เวกเตอร์, ดำเนินการตามลำดับนี้เรียกว่าเวกเตอร์ ความยาวซึ่งเป็นตัวเลข เท่ากับพื้นที่ของสี่เหลี่ยมด้านขนานสร้างขึ้นจากเวกเตอร์เหล่านี้ เวกเตอร์ ตั้งฉากกับเวกเตอร์และได้รับการกำกับเพื่อให้พื้นฐานมีการวางแนวที่ถูกต้อง: 
เรามาแจกแจงคำจำกัดความทีละส่วน มีอะไรน่าสนใจมากมายที่นี่!
ดังนั้นจึงสามารถเน้นประเด็นสำคัญต่อไปนี้ได้:
1) เวกเตอร์ดั้งเดิม ระบุด้วยลูกศรสีแดง ตามคำจำกัดความ ไม่ใช่แนวตรง. จะเหมาะสมที่จะพิจารณากรณีของเวกเตอร์คอลลิเนียร์ในภายหลังเล็กน้อย
2) ถ่ายเวกเตอร์ ตามลำดับที่กำหนดไว้อย่างเคร่งครัด: – "a" คูณด้วย "เป็น"ไม่ใช่ "เป็น" กับ "a" ผลลัพธ์ของการคูณเวกเตอร์คือ VECTOR ซึ่งระบุด้วยสีน้ำเงิน หากคูณเวกเตอร์ในลำดับย้อนกลับ เราจะได้เวกเตอร์ที่มีความยาวเท่ากันและมีทิศทางตรงกันข้าม (สีราสเบอร์รี่) นั่นคือความเท่าเทียมกันเป็นจริง 
.
3) ตอนนี้เรามาทำความคุ้นเคยกับความหมายทางเรขาคณิตของผลิตภัณฑ์เวกเตอร์กันดีกว่า นี่เป็นจุดสำคัญมาก! ความยาวของเวกเตอร์สีน้ำเงิน (และด้วยเหตุนี้จึงเป็นเวกเตอร์สีแดงเข้ม) มีค่าเท่ากับพื้นที่ของสี่เหลี่ยมด้านขนานที่สร้างขึ้นบนเวกเตอร์ ในรูป สี่เหลี่ยมด้านขนานนี้เป็นสีเทาดำ
บันทึก : การวาดภาพเป็นแผนผังและโดยธรรมชาติแล้วความยาวที่ระบุของผลิตภัณฑ์เวกเตอร์ไม่เท่ากับพื้นที่ของสี่เหลี่ยมด้านขนาน
ให้เรานึกถึงสูตรเรขาคณิตสูตรหนึ่ง: พื้นที่ของสี่เหลี่ยมด้านขนานเท่ากับผลคูณของด้านที่อยู่ติดกันและไซน์ของมุมระหว่างด้านเหล่านั้น. ดังนั้น จากสูตรข้างต้น สูตรคำนวณ LENGTH ของผลิตภัณฑ์เวกเตอร์จึงใช้ได้:
ฉันขอย้ำว่าสูตรนี้เกี่ยวกับ LENGTH ของเวกเตอร์ และไม่เกี่ยวกับเวกเตอร์นั้นเอง ความหมายเชิงปฏิบัติคืออะไร? และความหมายก็คือในปัญหาของเรขาคณิตวิเคราะห์ พื้นที่ของสี่เหลี่ยมด้านขนานมักพบผ่านแนวคิดของผลิตภัณฑ์เวกเตอร์:
ขอให้เราได้สูตรสำคัญที่สอง เส้นทแยงมุมของสี่เหลี่ยมด้านขนาน (เส้นประสีแดง) แบ่งออกเป็นสามเหลี่ยมสองรูปเท่าๆ กัน ดังนั้นจึงสามารถหาพื้นที่ของสามเหลี่ยมที่สร้างบนเวกเตอร์ (การแรเงาสีแดง) ได้โดยใช้สูตร:
4) ข้อเท็จจริงที่สำคัญไม่แพ้กันก็คือ เวกเตอร์นั้นตั้งฉากกับเวกเตอร์ นั่นก็คือ 
. แน่นอนว่า เวกเตอร์ที่มีทิศทางตรงกันข้าม (ลูกศรราสเบอร์รี่) ก็มีตั้งฉากกับเวกเตอร์ดั้งเดิมเช่นกัน
5) เวกเตอร์ถูกกำหนดทิศทางเช่นนั้น พื้นฐานมันมี ขวาปฐมนิเทศ. ในบทเรียนเกี่ยวกับ การเปลี่ยนไปสู่พื้นฐานใหม่ฉันพูดรายละเอียดเพียงพอเกี่ยวกับ การวางแนวเครื่องบินและตอนนี้เราจะหาว่าการวางแนวของอวกาศคืออะไร ฉันจะอธิบายบนนิ้วของคุณ มือขวา. ประสานจิต นิ้วชี้ด้วยเวกเตอร์และ นิ้วกลางด้วยเวกเตอร์ นิ้วนางและนิ้วก้อยกดมันลงบนฝ่ามือของคุณ ผลที่ตามมา นิ้วหัวแม่มือ– ผลิตภัณฑ์เวกเตอร์จะค้นหาขึ้น นี่เป็นพื้นฐานที่ถูกต้อง (นี่คืออันนี้ในรูป) ตอนนี้เปลี่ยนเวกเตอร์ ( นิ้วชี้และนิ้วกลาง) ในบางสถานที่ ผลก็คือ นิ้วหัวแม่มือจะหมุน และผลิตภัณฑ์เวกเตอร์จะมองลงมาแล้ว นี่เป็นพื้นฐานที่ถูกต้องเช่นกัน คุณอาจมีคำถาม: พื้นฐานใดที่ออกจากการปฐมนิเทศ? “กำหนด” ให้เป็นนิ้วเดียวกัน มือซ้ายเวกเตอร์ และรับพื้นฐานด้านซ้ายและการวางแนวด้านซ้ายของปริภูมิ (ในกรณีนี้นิ้วหัวแม่มือจะอยู่ในทิศทางของเวกเตอร์ด้านล่าง). หากพูดเป็นรูปเป็นร่าง ฐานเหล่านี้จะ "บิด" หรือปรับทิศทางพื้นที่ไปในทิศทางที่ต่างกัน และแนวคิดนี้ไม่ควรถือเป็นสิ่งที่ลึกซึ้งหรือเป็นนามธรรม - ตัวอย่างเช่น การวางแนวของอวกาศถูกเปลี่ยนโดยกระจกธรรมดาที่สุด และหากคุณ "ดึงวัตถุที่สะท้อนออกจากกระจกมอง" ในกรณีทั่วไป จะไม่สามารถนำมารวมกับ "ต้นฉบับ" ได้ ยังไงก็ตาม ชูสามนิ้วขึ้นไปที่กระจกแล้ววิเคราะห์การสะท้อน ;-)
...ตอนนี้คุณรู้ดีแค่ไหนแล้ว ไปทางขวาและซ้ายฐานเพราะคำพูดของอาจารย์บางคนเกี่ยวกับการเปลี่ยนแปลงการวางแนวนั้นน่ากลัว =)
ผลคูณไขว้ของเวกเตอร์คอลลิเนียร์
มีการพูดคุยถึงคำจำกัดความโดยละเอียดแล้ว ยังคงต้องค้นหาว่าจะเกิดอะไรขึ้นเมื่อเวกเตอร์อยู่ในแนวเดียวกัน หากเวกเตอร์อยู่ในแนวเดียวกัน ก็สามารถวางพวกมันบนเส้นตรงเส้นเดียวได้ และสี่เหลี่ยมด้านขนานของเราก็จะ "พับ" ให้เป็นเส้นตรงเส้นเดียวด้วย ดังที่นักคณิตศาสตร์กล่าวว่า เสื่อมโทรมสี่เหลี่ยมด้านขนานมีค่าเท่ากับศูนย์ ตามสูตรเดียวกัน - ไซน์ของศูนย์หรือ 180 องศาเท่ากับศูนย์ ซึ่งหมายความว่าพื้นที่เป็นศูนย์
ดังนั้น ถ้า แล้ว 
และ 
. โปรดทราบว่าผลคูณเวกเตอร์นั้นมีค่าเท่ากับเวกเตอร์ศูนย์ แต่ในทางปฏิบัติมักถูกละเลยและเขียนไว้ว่ามันเท่ากับศูนย์ด้วย
กรณีพิเศษคือผลคูณไขว้ของเวกเตอร์กับตัวมันเอง:
เมื่อใช้ผลิตภัณฑ์เวกเตอร์ คุณสามารถตรวจสอบความเป็นเส้นตรงของเวกเตอร์สามมิติได้ และเราจะวิเคราะห์ปัญหานี้และอื่นๆ ด้วย
เพื่อแก้ตัวอย่างเชิงปฏิบัติที่คุณอาจต้องการ ตารางตรีโกณมิติเพื่อหาค่าของไซน์จากมัน
มาจุดไฟกันเถอะ:
ตัวอย่างที่ 1
ก) จงหาความยาวของผลคูณเวกเตอร์ของเวกเตอร์ ถ้า 
b) ค้นหาพื้นที่ของสี่เหลี่ยมด้านขนานที่สร้างขึ้นบนเวกเตอร์ ถ้า 
สารละลาย: ไม่ นี่ไม่ใช่การพิมพ์ผิด ฉันจงใจทำให้ข้อมูลเริ่มต้นในส่วนคำสั่งเหมือนกัน เพราะการออกแบบโซลูชั่นจะแตกต่างออกไป!
ก) ตามเงื่อนไขคุณต้องค้นหา ความยาวเวกเตอร์ (ผลคูณข้าม) ตามสูตรที่เกี่ยวข้อง:
คำตอบ:
หากคุณถูกถามเกี่ยวกับความยาว ในคำตอบเราจะระบุมิติ - หน่วย
b) ตามเงื่อนไขคุณต้องค้นหา สี่เหลี่ยมสี่เหลี่ยมด้านขนานที่สร้างจากเวกเตอร์ พื้นที่ของสี่เหลี่ยมด้านขนานนี้เป็นตัวเลขเท่ากับความยาวของผลคูณเวกเตอร์:
คำตอบ:
โปรดทราบว่าคำตอบไม่ได้พูดถึงผลิตภัณฑ์เวกเตอร์เลย เราถูกถามเกี่ยวกับ พื้นที่ของรูปดังนั้น มิติข้อมูลจึงเป็นหน่วยสี่เหลี่ยม
เรามักจะมองหาสิ่งที่เราต้องค้นหาตามเงื่อนไข และจากสิ่งนี้ เราจึงกำหนดสูตรขึ้นมา ชัดเจนคำตอบ. อาจดูเหมือนเป็นวรรณกรรมตามตัวอักษร แต่มีครูที่เป็นวรรณกรรมจำนวนมาก และงานที่ได้รับมอบหมายก็มีโอกาสดีที่จะถูกส่งกลับเพื่อแก้ไข แม้ว่านี่จะไม่ใช่การพูดเล่นที่ลึกซึ้งนัก แต่หากคำตอบไม่ถูกต้อง เราก็จะรู้สึกว่าบุคคลนั้นไม่เข้าใจสิ่งง่ายๆ และ/หรือไม่เข้าใจแก่นแท้ของงาน ประเด็นนี้จะต้องถูกควบคุมเสมอเมื่อแก้ไขปัญหาใดๆ ในคณิตศาสตร์ขั้นสูงและในวิชาอื่นๆ ด้วย
ตัวอักษรตัวใหญ่ “en” หายไปไหน? โดยหลักการแล้ว มันอาจจะแนบมากับโซลูชันเพิ่มเติมได้ แต่เพื่อที่จะย่อรายการให้สั้นลง ฉันไม่ได้ทำเช่นนี้ ฉันหวังว่าทุกคนจะเข้าใจสิ่งนั้นและเป็นการกำหนดสิ่งเดียวกัน
ตัวอย่างยอดนิยมสำหรับโซลูชัน DIY:
ตัวอย่างที่ 2
ค้นหาพื้นที่ของสามเหลี่ยมที่สร้างจากเวกเตอร์ถ้า 
สูตรการหาพื้นที่ของสามเหลี่ยมผ่านผลคูณเวกเตอร์มีระบุไว้ในความคิดเห็นต่อคำจำกัดความ คำตอบและคำตอบอยู่ท้ายบทเรียน
ในทางปฏิบัติ งานนี้เป็นเรื่องธรรมดามาก โดยทั่วไปแล้ว รูปสามเหลี่ยมสามารถทรมานคุณได้
เพื่อแก้ไขปัญหาอื่น ๆ เราจะต้อง:
คุณสมบัติของผลิตภัณฑ์เวกเตอร์ของเวกเตอร์
เราได้พิจารณาคุณสมบัติบางอย่างของผลิตภัณฑ์เวกเตอร์แล้ว แต่ฉันจะรวมคุณสมบัติเหล่านี้ไว้ในรายการนี้
สำหรับเวกเตอร์ที่กำหนดเองและตัวเลขที่กำหนดเอง คุณสมบัติต่อไปนี้เป็นจริง:
1) ในแหล่งข้อมูลอื่นๆ รายการนี้มักจะไม่ได้เน้นในคุณสมบัติ แต่มีความสำคัญมากในแง่การปฏิบัติ ดังนั้นปล่อยให้มันเป็นไป
2) 
– ทรัพย์สินดังกล่าวยังกล่าวถึงข้างต้นบางครั้งเรียกว่า การต่อต้านคอมมิวทิตี. กล่าวอีกนัยหนึ่ง ลำดับของเวกเตอร์มีความสำคัญ
3) – เชื่อมโยงหรือ เชื่อมโยงกฎหมายผลิตภัณฑ์เวกเตอร์ ค่าคงที่สามารถเคลื่อนย้ายออกไปนอกผลคูณเวกเตอร์ได้อย่างง่ายดาย จริงๆ แล้วพวกเขาควรทำอะไรที่นั่น?
4) – การจำหน่ายหรือ การกระจายกฎหมายผลิตภัณฑ์เวกเตอร์ ไม่มีปัญหาในการเปิดวงเล็บเช่นกัน
เพื่อสาธิต ลองดูตัวอย่างสั้นๆ:
ตัวอย่างที่ 3
ค้นหาว่า 
สารละลาย:เงื่อนไขนี้จำเป็นต้องค้นหาความยาวของผลคูณเวกเตอร์อีกครั้ง มาวาดภาพจิ๋วของเรากันเถอะ: 
(1) ตามกฎการเชื่อมโยง เราใช้ค่าคงที่อยู่นอกขอบเขตของผลิตภัณฑ์เวกเตอร์
(2) เราใช้ค่าคงที่ภายนอกโมดูล และโมดูล "กิน" เครื่องหมายลบ ความยาวต้องไม่เป็นลบ
(3) ส่วนที่เหลือชัดเจน
คำตอบ: 
ถึงเวลาเพิ่มฟืนลงในกองไฟแล้ว:
ตัวอย่างที่ 4
คำนวณพื้นที่ของสามเหลี่ยมที่สร้างจากเวกเตอร์ถ้า 
สารละลาย: หาพื้นที่ของสามเหลี่ยมโดยใช้สูตร 
. สิ่งที่จับได้ก็คือเวกเตอร์ "tse" และ "de" นั้นถูกนำเสนอเป็นผลรวมของเวกเตอร์ อัลกอริทึมที่นี่เป็นมาตรฐานและค่อนข้างชวนให้นึกถึงตัวอย่างหมายเลข 3 และ 4 ของบทเรียน ผลคูณดอทของเวกเตอร์. เพื่อความชัดเจน เราจะแบ่งวิธีแก้ปัญหาออกเป็นสามขั้นตอน:
1) ในขั้นตอนแรก เราแสดงผลคูณเวกเตอร์ผ่านผลคูณเวกเตอร์ อันที่จริง ลองเขียนเวกเตอร์ในรูปของเวกเตอร์กัน. ยังไม่มีคำว่ายาว!
(1) แทนนิพจน์ของเวกเตอร์
(2) ใช้กฎการกระจาย เราจะเปิดวงเล็บตามกฎการคูณพหุนาม
(3) การใช้กฎเชื่อมโยง เราย้ายค่าคงที่ทั้งหมดไปไกลกว่าผลคูณเวกเตอร์ ด้วยประสบการณ์เพียงเล็กน้อยก็สามารถดำเนินการขั้นตอนที่ 2 และ 3 พร้อมๆ กันได้
(4) เทอมแรกและเทอมสุดท้ายมีค่าเท่ากับศูนย์ (เวกเตอร์ศูนย์) เนื่องจากคุณสมบัติที่ดี ในระยะที่สอง เราใช้คุณสมบัติของการต่อต้านการเปลี่ยนแปลงของผลิตภัณฑ์เวกเตอร์:
(5) เรานำเสนอข้อกำหนดที่คล้ายกัน
เป็นผลให้เวกเตอร์กลายเป็นเวกเตอร์ซึ่งเป็นสิ่งที่จำเป็นจะต้องทำให้สำเร็จ: 
2) ในขั้นตอนที่สอง เราจะหาความยาวของผลคูณเวกเตอร์ที่เราต้องการ การดำเนินการนี้คล้ายกับตัวอย่างที่ 3: 
3) ค้นหาพื้นที่ของสามเหลี่ยมที่ต้องการ: 
ขั้นที่ 2-3 ของการแก้ปัญหาสามารถเขียนเป็นบรรทัดเดียวได้
คำตอบ:
ปัญหาที่พิจารณานั้นค่อนข้างบ่อยในการทดสอบ นี่คือตัวอย่างสำหรับการแก้ไขด้วยตัวเอง:
ตัวอย่างที่ 5
ค้นหาว่า
คำตอบสั้น ๆ และคำตอบในตอนท้ายของบทเรียน มาดูกันว่าคุณใส่ใจแค่ไหนเมื่อศึกษาตัวอย่างก่อนหน้านี้ ;-)
ผลคูณไขว้ของเวกเตอร์ในพิกัด
ระบุไว้ตามหลักออร์โธนอร์มอล แสดงโดยสูตร:
สูตรนั้นง่ายมาก: ในบรรทัดบนสุดของดีเทอร์มิแนนต์เราเขียนเวกเตอร์พิกัดในบรรทัดที่สองและสามเรา "ใส่" พิกัดของเวกเตอร์แล้วใส่ ตามลำดับที่เข้มงวด– ขั้นแรกพิกัดของเวกเตอร์ “ve” ตามด้วยพิกัดของเวกเตอร์ “double-ve” หากจำเป็นต้องคูณเวกเตอร์ในลำดับอื่น ควรสลับแถว: 
ตัวอย่างที่ 10
ตรวจสอบว่าเวกเตอร์อวกาศต่อไปนี้เป็นเส้นตรงหรือไม่:
ก)
ข) 
สารละลาย: การตรวจสอบจะขึ้นอยู่กับข้อความใดข้อความหนึ่งในบทเรียนนี้: หากเวกเตอร์อยู่ในแนวเดียวกัน ผลคูณของเวกเตอร์จะเท่ากับศูนย์ (เวกเตอร์ศูนย์): 
.
ก) ค้นหาผลิตภัณฑ์เวกเตอร์: 
ดังนั้นเวกเตอร์จึงไม่อยู่ในแนวเดียวกัน
b) ค้นหาผลิตภัณฑ์เวกเตอร์: 
คำตอบ: ก) ไม่ใช่เส้นตรง b)
นี่อาจเป็นข้อมูลพื้นฐานทั้งหมดเกี่ยวกับผลคูณเวกเตอร์ของเวกเตอร์
ส่วนนี้จะไม่ใหญ่มาก เนื่องจากมีปัญหาเล็กน้อยในการใช้ผลคูณของเวกเตอร์ผสม ในความเป็นจริงทุกอย่างจะขึ้นอยู่กับคำจำกัดความ ความหมายทางเรขาคณิต และสูตรการทำงานสองสามสูตร
ผลคูณของเวกเตอร์คือผลคูณของเวกเตอร์สามตัว:
ดังนั้นพวกเขาจึงเข้าแถวเหมือนรถไฟและแทบรอไม่ไหวที่จะถูกระบุตัวตน
ประการแรก อีกครั้ง คำจำกัดความและรูปภาพ:
คำนิยาม: งานผสม ไม่ใช่ระนาบเวกเตอร์, ดำเนินการตามลำดับนี้, เรียกว่า ปริมาตรที่ขนานกันสร้างขึ้นบนเวกเตอร์เหล่านี้ โดยมีเครื่องหมาย “+” หากฐานถูกต้อง และเครื่องหมาย “–” หากเหลือฐาน
มาวาดรูปกันเถอะ เส้นที่เรามองไม่เห็นนั้นถูกวาดด้วยเส้นประ: 
มาดำดิ่งสู่คำจำกัดความ:
2) ถ่ายเวกเตอร์ ในลำดับที่แน่นอนนั่นคือการจัดเรียงเวกเตอร์ในผลิตภัณฑ์ใหม่ตามที่คุณอาจเดาได้จะไม่เกิดขึ้นโดยไม่มีผลกระทบ
3) ก่อนที่จะแสดงความคิดเห็นเกี่ยวกับความหมายทางเรขาคณิต ฉันจะทราบข้อเท็จจริงที่ชัดเจน: ผลคูณผสมของเวกเตอร์คือ NUMBER: . ในวรรณกรรมด้านการศึกษาการออกแบบอาจแตกต่างกันเล็กน้อย ฉันคุ้นเคยกับการแสดงถึงผลิตภัณฑ์ผสมด้วย และผลลัพธ์ของการคำนวณด้วยตัวอักษร "pe"
A-ไพรเออรี่ ผลคูณที่ผสมคือปริมาตรของเส้นขนานสร้างขึ้นจากเวกเตอร์ (รูปวาดด้วยเวกเตอร์สีแดงและเส้นสีดำ) นั่นคือจำนวนเท่ากับปริมาตรของเส้นขนานที่กำหนด
บันทึก : ภาพวาดเป็นแผนผัง
4) ไม่ต้องกังวลเกี่ยวกับแนวคิดเรื่องการวางแนวของพื้นฐานและพื้นที่อีกต่อไป ความหมายของส่วนสุดท้ายคือสามารถเพิ่มเครื่องหมายลบลงในโวลุ่มได้ พูดง่ายๆ ก็คือ ผลิตภัณฑ์แบบผสมอาจเป็นค่าลบ:
โดยตรงจากคำจำกัดความตามสูตรในการคำนวณปริมาตรของเส้นขนานที่สร้างขึ้นบนเวกเตอร์
คำนิยาม. ผลคูณเวกเตอร์ของเวกเตอร์ a และเวกเตอร์ b เป็นเวกเตอร์ที่แสดงด้วยสัญลักษณ์ [α, b] (หรือ l x b) โดยที่ 1) ความยาวของเวกเตอร์ [a, b] เท่ากับ (p โดยที่ y คือ มุมระหว่างเวกเตอร์ a และ b ( รูปที่ 31) 2) เวกเตอร์ [a, b) ตั้งฉากกับเวกเตอร์ a และ b นั่นคือ ตั้งฉากกับระนาบของเวกเตอร์เหล่านี้ 3) เวกเตอร์ [a, b] ถูกชี้ทิศทางในลักษณะที่จากจุดสิ้นสุดของเวกเตอร์นี้ การหมุนที่สั้นที่สุดจาก a ถึง b จะเกิดขึ้นทวนเข็มนาฬิกา (รูปที่ 32) ข้าว. 32 รูปที่ 31 หรืออีกนัยหนึ่ง เวกเตอร์ a, b และ [a, b) รวมกันเป็นสามเวกเตอร์ทางขวามือ กล่าวคือ อยู่เช่นนิ้วหัวแม่มือ นิ้วชี้ และนิ้วกลางของมือขวา หากเวกเตอร์ a และ b เป็นเส้นตรง เราจะถือว่า [a, b] = 0 ตามนิยาม ความยาวของผลคูณเวกเตอร์จะเป็นตัวเลขเท่ากับพื้นที่ Sa ของสี่เหลี่ยมด้านขนาน (รูปที่ 33) สร้างจากผลคูณ เวกเตอร์ a และ b เป็นด้าน: 6.1 . คุณสมบัติของผลิตภัณฑ์เวกเตอร์ 1. ผลคูณเวกเตอร์จะเท่ากับเวกเตอร์ศูนย์ ถ้าหากเวกเตอร์ที่คูณอย่างน้อยหนึ่งตัวเป็นศูนย์ หรือเมื่อเวกเตอร์เหล่านี้เป็นเส้นตรง (หากเวกเตอร์ a และ b เป็นเส้นตรง แล้วมุมระหว่างเวกเตอร์ทั้งสองจะเป็น 0 หรือ 7r) สิ่งนี้สามารถหาได้ง่ายจากข้อเท็จจริงที่ว่า หากเราถือว่าเวกเตอร์ศูนย์เป็นแบบโคลินาร์กับเวกเตอร์ใดๆ เงื่อนไขสำหรับความเป็นเชิงเส้นของเวกเตอร์ a และ b ก็สามารถแสดงได้ดังนี้: 2. ผลคูณเวกเตอร์เป็นแบบต้านสับเปลี่ยน กล่าวคือ เสมอ . ที่จริงแล้ว เวกเตอร์ (a, b) มีความยาวเท่ากันและเป็นเส้นตรง ทิศทางของเวกเตอร์เหล่านี้อยู่ตรงข้ามกัน เนื่องจากจากจุดสิ้นสุดของเวกเตอร์ [a, b] การหมุนที่สั้นที่สุดจาก a ถึง b จะเกิดขึ้นในทิศทางทวนเข็มนาฬิกาและจากจุดสิ้นสุดของเวกเตอร์ [b, a] - ตามเข็มนาฬิกา (รูปที่. 34) 3. ผลคูณเวกเตอร์มีคุณสมบัติการกระจายสัมพันธ์กับการบวก 4. ตัวประกอบตัวเลข A สามารถดึงออกจากเครื่องหมายของผลิตภัณฑ์เวกเตอร์ 6.2 ผลคูณเวกเตอร์ของเวกเตอร์ที่ระบุโดยพิกัด ให้เวกเตอร์ a และ b ถูกระบุด้วยพิกัดของพวกมันในฐาน เมื่อใช้คุณสมบัติการกระจายของผลิตภัณฑ์เวกเตอร์ เราจะค้นหาผลคูณเวกเตอร์ของเวกเตอร์ที่กำหนดโดยพิกัด งานผสม. ให้เราเขียนผลคูณเวกเตอร์ของเวกเตอร์หน่วยพิกัด (รูปที่ 35): ดังนั้นสำหรับผลคูณเวกเตอร์ของเวกเตอร์ a และ b เราได้รับจากสูตร (3) นิพจน์ต่อไปนี้ สูตร (4) สามารถเขียนเป็นสัญลักษณ์ได้ รูปแบบที่จำง่ายหากเราใช้ดีเทอร์มิแนนต์ลำดับที่ 3: เมื่อขยายดีเทอร์มิแนนต์นี้ไปเหนือองค์ประกอบของแถวที่ 1 เราจะได้ (4) ตัวอย่าง. 1. หาพื้นที่ของสี่เหลี่ยมด้านขนานที่สร้างบนเวกเตอร์ พื้นที่ที่ต้องการ ดังนั้นเราจึงหา = ที่ไหน 2. ค้นหาพื้นที่ของสามเหลี่ยม (รูปที่ 36) เป็นที่แน่ชัดว่าพื้นที่ b"d ของสามเหลี่ยม OAO เท่ากับครึ่งหนึ่งของพื้นที่ S ของสี่เหลี่ยมด้านขนาน O AC B เมื่อคำนวณผลคูณเวกเตอร์ (a, b| ของเวกเตอร์ a = OA และ b = ob เราจะได้ดังนี้ หมายเหตุ ผลคูณเวกเตอร์ไม่เชื่อมโยง กล่าวคือ ความเท่าเทียมกัน ( (a, b),c) = [a, |b,c)) ไม่เป็นความจริงในกรณีทั่วไป ตัวอย่างเช่น สำหรับ a = ss j เรามี § 7. ผลคูณของเวกเตอร์แบบผสม ขอให้เรามีเวกเตอร์ a, b และ c สามตัว คูณเวกเตอร์ a และ 1> ในเวกเตอร์ ผลลัพธ์ที่ได้คือเวกเตอร์ [a, 1>] คูณมันเป็นสเกลาร์ด้วยเวกเตอร์ c: ( k b), c).ตัวเลข ([a, b], e) เรียกว่าผลคูณผสมของเวกเตอร์ a, b. c และเขียนแทนด้วยสัญลักษณ์ (a, 1), e) เวกเตอร์ a, b และ c ในกรณีนี้เรียกว่า coplanar) จากนั้นผลคูณผสม ([a, b], c) = 0 ซึ่งตามมาจากข้อเท็จจริงที่ว่าเวกเตอร์ [a, b| ตั้งฉากกับระนาบซึ่งมีเวกเตอร์ a และ 1 โกหก "และดังนั้นถึงเวกเตอร์ c. / หากจุด O, A, B, C ไม่อยู่ในระนาบเดียวกัน (เวกเตอร์ a, b และ c ไม่ใช่ coplanar) เราจะสร้างเส้นขนานที่ขอบ OA, OB และระบบปฏิบัติการ (รูปที่. 38 ก) ตามคำจำกัดความของผลิตภัณฑ์เวกเตอร์ เรามี (a,b) = ดังนั้น c โดยที่ So คือพื้นที่ของสี่เหลี่ยมด้านขนาน OADB และ c คือเวกเตอร์หน่วยที่ตั้งฉากกับเวกเตอร์ a และ b และที่ทำให้สาม a , b, c เป็นคนถนัดขวาเช่น เวกเตอร์ a, b และ c อยู่ในตำแหน่งตามลำดับเป็นนิ้วหัวแม่มือ นิ้วชี้ และนิ้วกลางของมือขวา (รูปที่ 38 b) เมื่อคูณทั้งสองข้างของความเท่าเทียมกันสุดท้ายทางขวาด้วยเวกเตอร์ c เราจะได้ผลคูณเวกเตอร์ของเวกเตอร์ที่กำหนดโดยพิกัด งานผสม. จำนวน pc c เท่ากับความสูง h ของขนานที่สร้างขึ้นโดยคำนึงถึงเครื่องหมาย "+" หากมุมระหว่างเวกเตอร์ c และ c เป็นแบบเฉียบพลัน (สาม a, b, c - ขวา) และด้วย "-" แสดงว่ามุมป้าน (สาม a, b, c - ซ้าย) ดังนั้น ผลคูณผสมของเวกเตอร์ a, b และ c เท่ากับปริมาตร V ของเส้นขนานที่สร้างขึ้นบนเวกเตอร์เหล่านี้เหมือนกับที่ขอบ ถ้า ทริปเปิล a, b, c ถูกต้องและ -V ถ้าสาม a , b, c - ซ้าย จากความหมายทางเรขาคณิตของผลิตภัณฑ์ผสม เราสามารถสรุปได้ว่าโดยการคูณเวกเตอร์ a, b และ c ที่เหมือนกันในลำดับอื่น เราจะได้ +7 หรือ -K เสมอ รูปเครื่องหมายของผู้ผลิต การอ้างอิง 38 จะขึ้นอยู่กับชนิดของเวกเตอร์คูณสามชนิดเท่านั้น - ขวาหรือซ้าย ถ้าเวกเตอร์ a, b, c ประกอบเป็นรูปสามตัวทางขวา แล้วเวกเตอร์สามตัว b, c, a และ c, a, b ก็จะเป็นสามทางทางขวาด้วย ในเวลาเดียวกันทั้งสามสาม b, a, c; a, c, b และ c, b, a - ซ้าย ดังนั้น (a,b, c) = (b,c, a) = (c,a,b) = -(b,a,c) = -(a,c,b) = -(c,b , ก) เราเน้นอีกครั้งว่าผลคูณผสมของเวกเตอร์จะเท่ากับศูนย์ก็ต่อเมื่อเวกเตอร์ที่คูณ a, b, c เป็นโคพลานาร์: (a, b, c เป็นโคพลานาร์) 7.2 ผลคูณผสมในพิกัด ให้เวกเตอร์ a, b, c ถูกกำหนดโดยพิกัดของมันบนพื้นฐาน i, j, k: a = (x\,y\,z]), b= (x2,y2>z2), c = (x3, uz, 23) ให้เราค้นหานิพจน์สำหรับผลิตภัณฑ์ผสม (a, b, c) เรามีผลคูณของเวกเตอร์แบบผสมที่ระบุโดยพิกัดของพวกมันบนพื้นฐาน i, J, k เท่ากับดีเทอร์มิแนนต์ลำดับที่สาม เส้นที่ประกอบด้วยพิกัดของเวกเตอร์ตัวแรก ตัวที่สอง และตัวที่สามตามลำดับ เงื่อนไขที่จำเป็นและเพียงพอสำหรับระนาบร่วมของเวกเตอร์ a y\, Z|), b = (хъ У2.22), с = (жз, з, 23) จะถูกเขียนในรูปแบบต่อไปนี้ У| z, ag2 y2 -2 =0 ตัวอย่างอูซ ตรวจสอบว่าเวกเตอร์ „ = (7,4,6), b = (2, 1,1), c = (19, II, 17) เป็นระนาบเดียวกันหรือไม่ เวกเตอร์ที่พิจารณาจะเป็น coplanar หรือไม่ใช่ coplanar ขึ้นอยู่กับว่าดีเทอร์มิแนนต์มีค่าเท่ากับศูนย์หรือไม่ เมื่อขยายเข้าไปในองค์ประกอบของแถวแรกเราจะได้ D = 7-6-4-15 + 6-3 = 0^ - เวกเตอร์ n, b, c เป็นระนาบเดียวกัน 7.3. ผลคูณกากบาทคู่ [a, [b, c]] เป็นเวกเตอร์ตั้งฉากกับเวกเตอร์ a และ [b, c] ดังนั้นจึงอยู่ในระนาบของเวกเตอร์ b และ c และสามารถขยายเป็นเวกเตอร์เหล่านี้ได้ แสดงว่าสูตร [a, [!>, c]] = b(a, e) - c(a, b) ใช้ได้ แบบฝึกหัด 1. เวกเตอร์สามตัว AB = c, Ж? = o และ CA = b ทำหน้าที่เป็นด้านของสามเหลี่ยม จงเขียนในรูปของเวกเตอร์ a, b และ c ที่ตรงกับค่ามัธยฐาน AM, DN, CP ของรูปสามเหลี่ยม 2. เงื่อนไขใดที่เวกเตอร์ p และ q ต้องเชื่อมต่อเข้าด้วยกัน เพื่อให้เวกเตอร์ p + q แบ่งมุมระหว่างพวกมันออกเป็นสองส่วน? สันนิษฐานว่าเวกเตอร์ทั้งสามมีความสัมพันธ์กับจุดกำเนิดร่วม 3. คำนวณความยาวของเส้นทแยงมุมของสี่เหลี่ยมด้านขนานที่สร้างบนเวกเตอร์ a = 5p + 2q และ b = p - 3q หากทราบว่า |p| = 2v/2, |q| = 3 H-(p7ci) = ฉ. 4. แสดงด้วย a และ b ด้านข้างของสี่เหลี่ยมขนมเปียกปูนที่ยื่นออกมาจากจุดยอดร่วม พิสูจน์ว่าเส้นทแยงมุมของสี่เหลี่ยมขนมเปียกปูนนั้นตั้งฉากกัน 5. คำนวณผลคูณสเกลาร์ของเวกเตอร์ a = 4i + 7j + 3k และ b = 31 - 5j + k 6. จงหาเวกเตอร์หน่วย a0 ขนานกับเวกเตอร์ a = (6, 7, -6) 7. จงหาเส้นโครงของเวกเตอร์ a = l+ j- kHa vector b = 21 - j - 3k 8. จงหาโคไซน์ของมุมระหว่างเวกเตอร์คือ “w, ถ้า A(-4,0,4), B(-1,6,7), C(1,10.9) 9. จงหาเวกเตอร์หน่วย p° ซึ่งตั้งฉากกับเวกเตอร์ a = (3, 6, 8) และแกน Ox พร้อมกัน 10. คำนวณไซน์ของมุมระหว่างเส้นทแยงมุมของสี่เหลี่ยมด้านขนานที่สร้างบนเวกเตอร์ a = 2i+J-k, b=i-3j + k ดังที่ด้านข้าง คำนวณความสูง h ของรูปสี่เหลี่ยมด้านขนานที่สร้างขึ้นบนเวกเตอร์ a = 31 + 2j - 5k, b = i- j + 4knc = i-3j + k ถ้ารูปสี่เหลี่ยมด้านขนานที่สร้างจากเวกเตอร์ a และ I ถูกใช้เป็นฐาน คำตอบ
แน่นอน ในกรณีของผลิตภัณฑ์เวกเตอร์ ลำดับการใช้เวกเตอร์มีความสำคัญ ยิ่งไปกว่านั้น
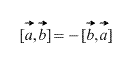
นอกจากนี้ โดยตรงจากคำจำกัดความ จะตามมาด้วยว่าสำหรับตัวประกอบสเกลาร์ k (ตัวเลข) ต่อไปนี้จะเป็นจริง:
ผลคูณไขว้ของเวกเตอร์คอลลิเนียร์เท่ากับเวกเตอร์ศูนย์ ยิ่งไปกว่านั้น ผลคูณไขว้ของเวกเตอร์สองตัวจะเป็นศูนย์ก็ต่อเมื่อพวกมันเป็นเส้นตรงเท่านั้น (ในกรณีที่หนึ่งในนั้นเป็นเวกเตอร์ศูนย์ จำเป็นต้องจำไว้ว่าเวกเตอร์ศูนย์นั้นอยู่ในแนวเดียวกันกับเวกเตอร์ใดๆ ตามคำจำกัดความ)
ผลิตภัณฑ์เวกเตอร์มี ทรัพย์สินจำหน่าย, นั่นคือ
การแสดงผลคูณเวกเตอร์ผ่านพิกัดของเวกเตอร์
ให้เวกเตอร์สองตัวมา
(วิธีค้นหาพิกัดของเวกเตอร์จากพิกัดของจุดเริ่มต้นและจุดสิ้นสุด - ดูบทความ Dot product of vector, item คำจำกัดความทางเลือกของ dot product หรือการคำนวณ dot product ของเวกเตอร์สองตัวที่ระบุโดยพิกัด)
ทำไมคุณถึงต้องการผลิตภัณฑ์เวกเตอร์?
มีหลายวิธีในการใช้ผลคูณไขว้ของเวกเตอร์สองตัว ตามที่เขียนไว้ข้างต้น โดยการคำนวณผลคูณไขว้ของเวกเตอร์สองตัว คุณจะทราบได้ว่าพวกมันอยู่ในแนวเดียวกันหรือไม่
หรือสามารถใช้เป็นวิธีคำนวณพื้นที่ของสี่เหลี่ยมด้านขนานที่สร้างจากเวกเตอร์เหล่านี้ได้ ตามคำนิยามความยาวของเวกเตอร์ที่ได้คือพื้นที่ของสี่เหลี่ยมด้านขนานที่กำหนด
นอกจากนี้ยังมีการใช้งานด้านไฟฟ้าและแม่เหล็กเป็นจำนวนมากเครื่องคิดเลขผลิตภัณฑ์เวกเตอร์ออนไลน์
หากต้องการค้นหาผลคูณสเกลาร์ของเวกเตอร์สองตัวโดยใช้เครื่องคิดเลขนี้ คุณต้องป้อนพิกัดของเวกเตอร์แรกในบรรทัดแรกตามลำดับ และป้อนพิกัดที่สองในบรรทัดที่สอง พิกัดของเวกเตอร์สามารถคำนวณได้จากพิกัดของจุดเริ่มต้นและจุดสิ้นสุด (ดูบทความ ผลคูณดอทของเวกเตอร์ รายการ คำจำกัดความอื่นของผลิตภัณฑ์ดอท หรือการคำนวณผลคูณดอทของเวกเตอร์สองตัวที่กำหนดโดยพิกัดของพวกมัน)
7.1. คำจำกัดความของผลิตภัณฑ์ข้าม
เวกเตอร์ a, b และ c ที่ไม่ใช่ระนาบระนาบสามตัว ถ่ายตามลำดับที่ระบุ สร้างแฝดสามทางขวา ถ้าจากจุดสิ้นสุดของเวกเตอร์ที่สาม c เห็นการหมุนที่สั้นที่สุดจากเวกเตอร์แรก a ถึงเวกเตอร์ b ที่สองถึง ทวนเข็มนาฬิกา และแฝดซ้ายถ้าตามเข็มนาฬิกา (ดูรูปที่ 16)
ผลคูณเวกเตอร์ของเวกเตอร์ a และเวกเตอร์ b เรียกว่าเวกเตอร์ c ซึ่ง:
1. ตั้งฉากกับเวกเตอร์ a และ b เช่น c ^ a และ c ^ ข ;
2. มีความยาวเป็นตัวเลขเท่ากับพื้นที่ของสี่เหลี่ยมด้านขนานที่สร้างบนเวกเตอร์ a และขเช่นเดียวกับด้านข้าง (ดูรูปที่ 17) เช่น
3. เวกเตอร์ a, b และ c ประกอบเป็นรูปสามเท่าของมือขวา
ผลคูณกากบาทเขียนแทน a x b หรือ [a,b] ความสัมพันธ์ต่อไปนี้ระหว่างเวกเตอร์หน่วยที่ฉันติดตามโดยตรงจากคำจำกัดความของผลิตภัณฑ์เวกเตอร์ เจและ เค(ดูรูปที่ 18):
ฉัน x เจ = k, เจ x k = ฉัน, k x i = เจ
ให้เราพิสูจน์เป็นตัวอย่างว่าฉัน xj = k
1) k ^ ฉัน, k ^ เจ ;
2) |k |=1 แต่ | ฉัน x เจ| = |ฉัน | |เจ | บาป(90°)=1;
3) เวกเตอร์ ผม, เจ และ เคสร้างสามด้านขวา (ดูรูปที่ 16)
7.2. คุณสมบัติของผลิตภัณฑ์ข้าม
1. เมื่อจัดเรียงปัจจัยใหม่ ผลิตภัณฑ์เวกเตอร์จะเปลี่ยนเครื่องหมาย เช่น และ xb =(b xa) (ดูรูปที่ 19)
เวกเตอร์ a xb และ b xa เป็นเส้นตรง มีโมดูลเดียวกัน (พื้นที่ของสี่เหลี่ยมด้านขนานยังคงไม่เปลี่ยนแปลง) แต่มีทิศทางตรงกันข้าม (สามเท่า a, b, xb และ a, b, b x a ในทิศทางตรงกันข้าม) นั่นคือ เอ๊กซ์บี = -(ขxa).
2. ผลคูณเวกเตอร์มีคุณสมบัติการรวมโดยคำนึงถึงปัจจัยสเกลาร์ เช่น l (a xb) = (l a) x b = a x (l b)
ให้ l >0 เวกเตอร์ l (a xb) ตั้งฉากกับเวกเตอร์ a และ b เวกเตอร์ ( ลขวาน ขยังตั้งฉากกับเวกเตอร์ a และ อีกด้วย ข(เวกเตอร์ ก, ลแต่นอนอยู่ในระนาบเดียวกัน) นี่หมายความว่าเวกเตอร์ ล(กxb) และ ( ลขวาน ขคอลลิเนียร์ เห็นได้ชัดว่าทิศทางของพวกเขาตรงกัน มีความยาวเท่ากัน:
นั่นเป็นเหตุผล ล(กxb)= ลเอ็กซ์บี ก็ได้รับการพิสูจน์ในลักษณะเดียวกันสำหรับ ล<0.
3. เวกเตอร์ที่ไม่เป็นศูนย์สองตัว a และ ขเป็นเส้นตรงก็ต่อเมื่อผลคูณเวกเตอร์ของพวกมันเท่ากับเวกเตอร์ศูนย์ นั่นคือ a ||b<=>และ xb = 0
โดยเฉพาะอย่างยิ่ง i *i =j *j =k *k =0
4. ผลิตภัณฑ์เวกเตอร์มีคุณสมบัติการกระจาย:
(ก+ข) xc = ก xc + ข xs
เราจะยอมรับโดยไม่มีข้อพิสูจน์
7.3. การแสดงผลคูณไขว้ในแง่ของพิกัด
เราจะใช้ตารางผลคูณของเวกเตอร์ i เจและเค:
ถ้าทิศทางของเส้นทางที่สั้นที่สุดจากเวกเตอร์แรกไปวินาทีตรงกับทิศทางของลูกศรผลคูณจะเท่ากับเวกเตอร์ที่สามหากไม่ตรงกันเวกเตอร์ที่สามจะถูกใช้เครื่องหมายลบ
ให้เวกเตอร์สองตัว a =a x i +a y ได้รับ เจ+ก เคและ ข = ข x ฉัน+บี เจ+บีซ เค. ลองหาผลคูณเวกเตอร์ของเวกเตอร์เหล่านี้โดยการคูณมันเป็นพหุนาม (ตามคุณสมบัติของผลคูณเวกเตอร์):
สูตรผลลัพธ์สามารถเขียนได้สั้นยิ่งขึ้น:
เนื่องจากด้านขวาของความเท่าเทียมกัน (7.1) สอดคล้องกับการขยายตัวของปัจจัยลำดับที่สามในแง่ขององค์ประกอบของแถวแรก ความเท่าเทียมกัน (7.2) นั้นง่ายต่อการจดจำ
7.4. การใช้งานบางส่วนของผลิตภัณฑ์ข้าม
การสร้างความสัมพันธ์เชิงเส้นของเวกเตอร์
การหาพื้นที่ของสี่เหลี่ยมด้านขนานและสามเหลี่ยม
ตามคำจำกัดความของผลิตภัณฑ์เวกเตอร์ของเวกเตอร์ กและข |a xb | =|a | * |b |sin g เช่น S คู่ = |a x b | ดังนั้น D S =1/2|a x b |
การหาโมเมนต์แรงรอบจุดหนึ่ง
ให้ออกแรงที่จุด A เอฟ =เอบีปล่อยมันไป เกี่ยวกับ- บางจุดในอวกาศ (ดูรูปที่ 20)
เป็นที่ทราบกันดีจากฟิสิกส์ว่า ช่วงเวลาแห่งพลัง เอฟ สัมพันธ์กับประเด็น เกี่ยวกับเรียกว่าเวกเตอร์ เอ็มซึ่งผ่านจุดนั้นไป เกี่ยวกับและ:
1) ตั้งฉากกับระนาบที่ผ่านจุดต่างๆ โอ้, ก, บี;
2) ตัวเลขเท่ากับผลคูณของแรงต่อแขน
3) สร้างรูปสามเหลี่ยมมุมฉากด้านขวาด้วยเวกเตอร์ OA และ A B
ดังนั้น M = OA x F
การหาความเร็วการหมุนเชิงเส้น
ความเร็ว โวลต์จุด M ของวัตถุแข็งเกร็งที่หมุนด้วยความเร็วเชิงมุม วรอบแกนคงที่ จะถูกกำหนดโดยสูตรของออยเลอร์ v =w xr โดยที่ r =OM โดยที่ O คือจุดคงที่ของแกน (ดูรูปที่ 21)
