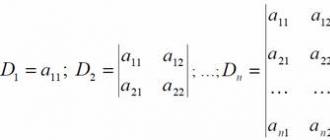กฎสำหรับการเข้าฟังก์ชั่น:
ฟังก์ชันหาอนุพันธ์ได้อย่างต่อเนื่องสองครั้ง f(x) คือนูน (เว้า) ถ้าหากเท่านั้น เมทริกซ์เฮสเซียนฟังก์ชัน f(x) เทียบกับ x นั้นเป็นค่าบวก (ลบ) แบบกึ่งแน่นอนสำหรับ x ทั้งหมด (ดูจุดสุดขั้วเฉพาะที่ของฟังก์ชันของตัวแปรหลายตัว)
ฟังก์ชั่นจุดวิกฤต:
- ถ้า Hessian เป็นค่าบวกที่แน่นอน ดังนั้น x 0 คือจุดต่ำสุดเฉพาะที่ของฟังก์ชัน f(x)
- ถ้า Hessian เป็นลบแน่นอน ดังนั้น x 0 คือจุดสูงสุดเฉพาะที่ของฟังก์ชัน f(x)
- ถ้า Hessian ไม่ใช่เครื่องหมายที่แน่นอน (รับทั้งค่าบวกและค่าลบ) และไม่เสื่อมลง (det G(f) ≠ 0) ดังนั้น x 0 คือจุดอานของฟังก์ชัน f(x)
เกณฑ์สำหรับความแน่นอนของเมทริกซ์ (ทฤษฎีบทของซิลเวสเตอร์)
ความมั่นใจเชิงบวก:- องค์ประกอบแนวทแยงทั้งหมดของเมทริกซ์จะต้องเป็นบวก
- ผู้ผ่านการคัดเลือกหลักทั้งหมดจะต้องเป็นค่าบวก
ความกึ่งแน่นอนเชิงบวก:
- องค์ประกอบในแนวทแยงทั้งหมดไม่เป็นลบ
- ปัจจัยหลักทั้งหมดไม่เป็นลบ
เมทริกซ์สมมาตรสี่เหลี่ยมของลำดับ n องค์ประกอบที่เป็นอนุพันธ์ย่อยของฟังก์ชันวัตถุประสงค์ลำดับที่สอง เรียกว่าเมทริกซ์เฮสเซียนและถูกกำหนดไว้:
เพื่อให้เมทริกซ์สมมาตรมีค่าแน่นอนเป็นบวก จำเป็นอย่างยิ่งและเพียงพอที่เมทริกซ์ย่อยในแนวทแยงทั้งหมดจะเป็นค่าบวก กล่าวคือ 
สำหรับเมทริกซ์ A = (a ij) เป็นบวก
ความแน่นอนเชิงลบ.
เพื่อให้เมทริกซ์สมมาตรมีค่าแน่นอนเป็นลบ จำเป็นและเพียงพอที่อสมการต่อไปนี้จะเกิดขึ้น:
(-1) k D k > 0, เค=1,..,น.
กล่าวอีกนัยหนึ่ง เพื่อให้รูปกำลังสองเป็น เชิงลบแน่นอนจำเป็นและเพียงพอที่สัญญาณของไมเนอร์เชิงมุมของเมทริกซ์รูปแบบกำลังสองสลับกัน โดยเริ่มจากเครื่องหมายลบ ตัวอย่างเช่น สำหรับตัวแปรสองตัว D 1< 0, D 2 > 0.
ถ้า Hessian เป็นแบบกึ่งแน่นอน นี่อาจเป็นจุดเปลี่ยนเว้าเช่นกัน จำเป็นต้องมีการวิจัยเพิ่มเติม ซึ่งสามารถดำเนินการได้โดยใช้ตัวเลือกใดตัวเลือกหนึ่งต่อไปนี้:
- การสั่งซื้อลดลง. มีการเปลี่ยนตัวแปร ตัวอย่างเช่น สำหรับฟังก์ชันของตัวแปรสองตัว มันคือ y=x ด้วยเหตุนี้เราจึงได้ฟังก์ชันของตัวแปร x ตัวเดียว ต่อไป เราจะตรวจสอบพฤติกรรมของฟังก์ชันบนเส้น y=x และ y=-x หากในกรณีแรกฟังก์ชันที่จุดที่กำลังศึกษาจะมีค่าต่ำสุด และในกรณีอื่นมีค่าสูงสุด (หรือกลับกัน) จุดที่กำลังศึกษาคือจุดอาน
- การค้นหาค่าลักษณะเฉพาะของ Hessian ถ้าค่าทั้งหมดเป็นบวก ฟังก์ชัน ณ จุดที่กำลังศึกษาจะมีค่าต่ำสุด ถ้าค่าทั้งหมดเป็นลบ ก็จะมีค่าสูงสุด
- ศึกษาฟังก์ชัน f(x) ในบริเวณใกล้จุด ε ตัวแปร x ถูกแทนที่ด้วย x 0 +ε ถัดไป จำเป็นต้องพิสูจน์ว่าฟังก์ชัน f(x 0 +ε) ของตัวแปรหนึ่งตัว ε นั้นมากกว่าศูนย์ (จากนั้น x 0 คือจุดต่ำสุด) หรือน้อยกว่าศูนย์ (จากนั้น x 0 คือจุดสูงสุด)
บันทึก. การค้นหา เฮสเซียนผกผันก็เพียงพอแล้วที่จะหาเมทริกซ์ผกผัน
ตัวอย่างหมายเลข 1 ฟังก์ชันใดต่อไปนี้นูนหรือเว้า: f(x) = 8x 1 2 +4x 1 x 2 +5x 2 2 .
สารละลาย. 1. ลองหาอนุพันธ์ย่อยกัน 
2. มาแก้ระบบสมการกัน
-4x 1 +4x 2 +2 = 0
4x 1 -6x 2 +6 = 0
เราได้รับ:
ก) จากสมการแรกเราแสดง x 1 และแทนลงในสมการที่สอง:
x 2 = x 2 + 1/2
-2x 2 +8 = 0
โดยที่ x 2 = 4
เราแทนที่ค่าเหล่านี้ x 2 ลงในนิพจน์สำหรับ x 1 เราได้รับ: x 1 = 9/2
จำนวนจุดวิกฤตคือ 1
ม 1 (9 / 2 ;4)
3. ลองหาอนุพันธ์ย่อยอันดับสองกัน
4. ให้เราคำนวณมูลค่าของอนุพันธ์บางส่วนอันดับสองที่จุดวิกฤต M(x 0 ;y 0)
เราคำนวณค่าสำหรับจุด M 1 (9 / 2 ;4) 
เราสร้างเมทริกซ์ Hessian:
ง 1 = ก 11< 0, D 2 = 8 > 0
เนื่องจากผู้เยาว์ในแนวทแยงมีสัญญาณที่แตกต่างกัน จึงไม่สามารถพูดเกี่ยวกับความนูนหรือความเว้าของฟังก์ชันได้
การแนะนำ…………………………………………………………….......................... ........ ................3
1 ข้อมูลทางทฤษฎีเกี่ยวกับรูปแบบกำลังสอง……………………………4
1.1 คำจำกัดความของรูปแบบกำลังสอง…………………………….…4
1.2 การลดรูปแบบกำลังสองให้เป็นรูปแบบมาตรฐาน………………...6
1.3 กฎความเฉื่อย………………………………………………………….….11
1.4 รูปแบบที่แน่นอนเชิงบวก……………………………………...18
2 การใช้รูปแบบกำลังสองเชิงปฏิบัติ …………………22
2.1 การแก้ปัญหาทั่วไป………………………………………………………………22
2.2 งานสำหรับการแก้ปัญหาอิสระ……...………………….………...26
2.3 งานทดสอบ………………………………………………………………...27
สรุป………….……………………...…………………29
รายการวรรณกรรมที่ใช้แล้ว…………………………………………...30
การแนะนำ
เริ่มแรก ทฤษฎีรูปแบบกำลังสองใช้เพื่อศึกษาเส้นโค้งและพื้นผิวที่กำหนดโดยสมการอันดับสองที่มีตัวแปรสองหรือสามตัว ต่อมาทฤษฎีนี้พบการประยุกต์อื่นๆ โดยเฉพาะอย่างยิ่ง เมื่อสร้างแบบจำลองกระบวนการทางคณิตศาสตร์ทางคณิตศาสตร์ ฟังก์ชันวัตถุประสงค์อาจมีเงื่อนไขกำลังสอง การประยุกต์รูปแบบกำลังสองจำนวนมากจำเป็นต้องมีการสร้างทฤษฎีทั่วไปเมื่อจำนวนตัวแปรเท่ากับค่าใดๆ
และสัมประสิทธิ์ของรูปกำลังสองไม่ใช่จำนวนจริงเสมอไปทฤษฎีรูปกำลังสองได้รับการพัฒนาครั้งแรกโดยนักคณิตศาสตร์ชาวฝรั่งเศส ลากรองจ์ ซึ่งเป็นเจ้าของแนวคิดมากมายในทฤษฎีนี้ โดยเฉพาะอย่างยิ่ง เขาได้แนะนำแนวคิดที่สำคัญของรูปแบบที่ลดลง ด้วยความช่วยเหลือซึ่งเขาได้พิสูจน์ความจำกัดของจำนวนคลาสของ รูปแบบกำลังสองไบนารีของการแบ่งแยกที่กำหนด จากนั้นทฤษฎีนี้ได้รับการขยายอย่างมีนัยสำคัญโดยเกาส์ซึ่งแนะนำแนวคิดใหม่ ๆ มากมายบนพื้นฐานที่เขาสามารถรับการพิสูจน์ทฤษฎีบทที่ยากและลึกซึ้งของทฤษฎีจำนวนที่หลบเลี่ยงรุ่นก่อนของเขาในสาขานี้
วัตถุประสงค์ของงานคือเพื่อศึกษาประเภทของรูปแบบกำลังสองและวิธีการลดรูปแบบกำลังสองให้เป็นรูปแบบมาตรฐาน
งานนี้กำหนดงานต่อไปนี้: เลือกวรรณกรรมที่จำเป็น พิจารณาคำจำกัดความ แก้ไขปัญหาจำนวนหนึ่ง และเตรียมการทดสอบ
1 ข้อมูลทางทฤษฎีเกี่ยวกับรูปแบบกำลังสอง
1.1 คำจำกัดความของรูปแบบกำลังสอง
รูปร่างกำลังสอง
ของสิ่งที่ไม่รู้คือผลรวม แต่ละเทอมจะเป็นกำลังสองของสิ่งที่ไม่รู้เหล่านี้ หรือผลคูณของสิ่งที่ไม่รู้สองอันที่แตกต่างกัน รูปแบบกำลังสองมีสองรูปแบบ: จำนวนจริงและจำนวนเชิงซ้อน ขึ้นอยู่กับว่าสัมประสิทธิ์เป็นจำนวนจริงหรือจำนวนเชิงซ้อนแสดงถึงสัมประสิทธิ์ที่
ผ่าน และเมื่อผลิต
, ผ่าน 
รูปแบบกำลังสองสามารถแสดงเป็น: จากค่าสัมประสิทธิ์
มันเป็นไปได้ที่จะสร้างเมทริกซ์จตุรัสของลำดับ; มันถูกเรียกว่าเมทริกซ์รูปกำลังสอง และอันดับของมันถูกเรียกว่าอันดับของรูปกำลังสอง โดยเฉพาะอย่างยิ่งหาก , โดยที่ นั่นคือเมทริกซ์ไม่เสื่อมแล้วรูปแบบกำลังสองจะเรียกว่าไม่เสื่อม สำหรับเมทริกซ์สมมาตรของลำดับใดๆ สามารถระบุได้ในรูปแบบกำลังสองที่กำหนดไว้อย่างสมบูรณ์:
(1.1) - ไม่ทราบข้อมูล ซึ่งมีองค์ประกอบเมทริกซ์ที่มีค่าสัมประสิทธิ์ ให้เราแสดงโดย
คอลัมน์ที่ประกอบด้วยสิ่งที่ไม่รู้จัก: . เป็นเมทริกซ์ที่มีแถวและหนึ่งคอลัมน์ เมื่อย้ายเมทริกซ์นี้ เราจะได้เมทริกซ์ดังนี้
, ประกอบด้วยบรรทัดเดียว รูปแบบกำลังสอง (1.1) พร้อมเมทริกซ์
ตอนนี้สามารถเขียนเป็นผลิตภัณฑ์ได้แล้ว:.1.2 การลดลงเป็นรูปแบบกำลังสอง
สู่มุมมองแบบบัญญัติ
สมมุติว่าเป็นรูปกำลังสอง
จากสิ่งไม่รู้ได้ลดลงแล้วโดยการแปลงเชิงเส้นที่ไม่เสื่อมลงเป็นรูปแบบมาตรฐาน ซึ่งสิ่งไม่รู้ใหม่อยู่ที่ไหน ค่าสัมประสิทธิ์บางส่วนอาจเป็นศูนย์ ให้เราพิสูจน์ว่าจำนวนสัมประสิทธิ์ที่ไม่ใช่ศูนย์จำเป็นต้องเท่ากับอันดับของแบบฟอร์ม เมทริกซ์ของรูปแบบกำลังสองนี้มีรูปแบบเส้นทแยงมุม
,
และข้อกำหนดที่เมทริกซ์นี้มีอันดับ
เทียบเท่ากับการสันนิษฐานว่าเส้นทแยงมุมหลักมีองค์ประกอบที่ไม่ใช่ศูนย์ทุกประการทฤษฎีบท.รูปแบบกำลังสองใดๆ สามารถลดลงเป็นรูปแบบมาตรฐานโดยการแปลงเชิงเส้นที่ไม่เสื่อมลง หากพิจารณารูปแบบกำลังสองจริง ค่าสัมประสิทธิ์ทั้งหมดของการแปลงเชิงเส้นที่ระบุจะถือเป็นจำนวนจริงได้
การพิสูจน์. ทฤษฎีบทนี้เป็นจริงสำหรับกรณีของรูปแบบกำลังสองในรูปแบบที่ไม่รู้จัก เนื่องจากรูปแบบดังกล่าวใดๆ ก็มีรูปแบบ
ซึ่งเป็นรูปแบบบัญญัติ ให้เราแนะนำการพิสูจน์โดยการอุปนัย นั่นคือ พิสูจน์ทฤษฎีบทของรูปแบบกำลังสองในรูปแบบไม่ทราบค่า โดยพิจารณาว่าได้รับการพิสูจน์แล้วสำหรับรูปแบบที่ไม่ทราบจำนวนน้อยกว่าให้รูปกำลังสอง (1.1) ของ
เมื่อแก้ไขปัญหาต่างๆ ที่ประยุกต์ มักจำเป็นต้องศึกษารูปแบบกำลังสอง
คำนิยาม.รูปแบบกำลังสอง L(, x 2, ..., xn) ของตัวแปร n ตัวคือผลรวม ซึ่งแต่ละพจน์จะเป็นกำลังสองของตัวแปรตัวใดตัวหนึ่งหรือผลคูณของตัวแปรสองตัวที่ต่างกันซึ่งมีค่าสัมประสิทธิ์ที่แน่นอน:
ลิตร( ,x 2 ,...,xn) =
เราถือว่าสัมประสิทธิ์ของรูปกำลังสองเป็นจำนวนจริง และ
เมทริกซ์ A = () (i, j = 1, 2, ..., n) ที่ประกอบด้วยสัมประสิทธิ์เหล่านี้ เรียกว่าเมทริกซ์รูปกำลังสอง
ในสัญลักษณ์เมทริกซ์ รูปแบบกำลังสองมีรูปแบบ: L = X"AX โดยที่ X = (x 1, x 2,..., x n)" - เมทริกซ์คอลัมน์ของตัวแปร
ตัวอย่างที่ 8.1
เขียนรูปกำลังสอง L( , x 2 , x 3) = ในรูปแบบเมทริกซ์
ลองหาเมทริกซ์ที่มีรูปแบบกำลังสองกัน องค์ประกอบในแนวทแยงของมันเท่ากับค่าสัมประสิทธิ์ของตัวแปรกำลังสองนั่นคือ 4, 1, -3 และองค์ประกอบอื่นๆ - ถึงครึ่งหนึ่งของสัมประสิทธิ์ที่สอดคล้องกันของรูปแบบกำลังสอง นั่นเป็นเหตุผล
ยาว=( , x 2 , x 3) 
.
ด้วยการแปลงเชิงเส้นที่ไม่เสื่อมลง X = CY เมทริกซ์ของรูปแบบกำลังสองจะอยู่ในรูปแบบ: A * = C "AC (*)
ตัวอย่างที่ 8.2
เมื่อกำหนดรูปแบบกำลังสอง L(x x, x 2) =2x 1 2 +4x 1 x 2 -3 ค้นหารูปแบบกำลังสอง L(y 1 ,y 2) ที่ได้จากการแปลงเชิงเส้นที่กำหนด = 2у 1 - 3ปี 2 , x 2 = ย 1 + ย 2
เมทริกซ์ของรูปแบบกำลังสองที่กำหนดคือ A= และเมทริกซ์การแปลงเชิงเส้นคือ
ค = . ดังนั้นตาม (*) เมทริกซ์ของรูปแบบกำลังสองที่ต้องการ
และรูปแบบกำลังสองดูเหมือน
L(ปี 1, ปี 2) =
.
ควรสังเกตว่าด้วยการแปลงเชิงเส้นที่เลือกสรรมาอย่างดี รูปแบบของรูปแบบกำลังสองสามารถทำให้ง่ายขึ้นอย่างมาก
คำนิยาม.รูปแบบกำลังสอง L(,x 2,...,x n) = เรียกว่ารูปแบบบัญญัติ (หรือมีรูปแบบมาตรฐาน) ถ้าสัมประสิทธิ์ทั้งหมด = 0 สำหรับ i¹j:
ล= 
และเมทริกซ์ของมันคือเส้นทแยงมุม
ทฤษฎีบทต่อไปนี้เป็นจริง
ทฤษฎีบท.รูปแบบกำลังสองใดๆ สามารถถูกลดให้เป็นรูปแบบมาตรฐานได้โดยใช้การแปลงตัวแปรเชิงเส้นที่ไม่เสื่อมลง
ตัวอย่าง 8.3
ลดรูปแบบกำลังสองให้เป็นรูปแบบมาตรฐาน
ยาว( , x 2 , x 3) =
ขั้นแรก เราเลือกกำลังสองที่สมบูรณ์ของตัวแปร ซึ่งสัมประสิทธิ์ของกำลังสองแตกต่างจากศูนย์:
ตอนนี้เราเลือกกำลังสองที่สมบูรณ์แบบสำหรับตัวแปรที่มีค่าสัมประสิทธิ์แตกต่างจากศูนย์:
ดังนั้น การแปลงเชิงเส้นแบบไม่เสื่อม
ลดรูปแบบกำลังสองนี้ให้เป็นรูปแบบมาตรฐาน: 
รูปแบบมาตรฐานของรูปแบบกำลังสองไม่ได้ถูกกำหนดไว้โดยเฉพาะ เนื่องจากรูปแบบกำลังสองเดียวกันสามารถถูกลดให้เป็นรูปแบบมาตรฐานได้หลายวิธี อย่างไรก็ตาม รูปแบบมาตรฐานที่ได้รับจากวิธีการต่างๆ มีคุณสมบัติทั่วไปหลายประการ ให้เรากำหนดคุณสมบัติอย่างใดอย่างหนึ่งเหล่านี้เป็นทฤษฎีบท
ทฤษฎีบท (กฎความเฉื่อยของรูปแบบกำลังสอง)จำนวนพจน์ที่มีค่าสัมประสิทธิ์บวก (ลบ) ของรูปแบบกำลังสองไม่ได้ขึ้นอยู่กับวิธีการลดรูปแบบให้อยู่ในรูปแบบนี้
ควรสังเกตว่าอันดับของเมทริกซ์ของรูปแบบกำลังสองเท่ากับจำนวนสัมประสิทธิ์ที่ไม่ใช่ศูนย์ของรูปแบบบัญญัติและไม่เปลี่ยนแปลงภายใต้การแปลงเชิงเส้น
คำนิยาม.รูปแบบกำลังสอง L(, x 2, ..., xn) เรียกว่าบวก (ลบ) แน่นอนถ้าสำหรับค่าทั้งหมดของตัวแปรอย่างน้อยหนึ่งค่าที่ไม่ใช่ศูนย์
ยาว( , x 2 , ..., xn) > 0 (L( , x 2 , ..., xn)< 0).
ดังนั้น, ตัวอย่างเช่น, รูปแบบกำลังสอง 
เป็นบวกแน่นอน และรูปแบบเป็นลบแน่นอน
ทฤษฎีบท.เพื่อให้รูปแบบกำลังสอง L = X"AX เป็นบวก (ลบ) แน่นอนจำเป็นและเพียงพอที่ค่าลักษณะเฉพาะทั้งหมดของเมทริกซ์ A เป็นบวก (ลบ)
รูปร่างกำลังสอง f(x 1, x 2,...,x n) ของตัวแปร n ตัวคือผลรวม ซึ่งแต่ละพจน์จะเป็นกำลังสองของตัวแปรตัวใดตัวหนึ่ง หรือผลคูณของตัวแปรสองตัวที่ต่างกัน ซึ่งใช้ค่าสัมประสิทธิ์ที่แน่นอน: f (x 1, x 2, ...,x n) = (ก อิจ =จิ)
เมทริกซ์ A ที่ประกอบด้วยสัมประสิทธิ์เหล่านี้เรียกว่าเมทริกซ์รูปแบบกำลังสอง ก็เสมอกัน สมมาตรเมทริกซ์ (เช่น เมทริกซ์สมมาตรเกี่ยวกับเส้นทแยงมุมหลัก a ij = a ji)
ในรูปแบบเมทริกซ์ รูปแบบกำลังสองคือ f(X) = X T AX โดยที่
อย่างแท้จริง
ตัวอย่างเช่น ลองเขียนรูปกำลังสองในรูปแบบเมทริกซ์
เมื่อต้องการทำเช่นนี้ เราจะหาเมทริกซ์ที่มีรูปแบบกำลังสอง องค์ประกอบในแนวทแยงจะเท่ากับสัมประสิทธิ์ของตัวแปรกำลังสอง และองค์ประกอบที่เหลือจะเท่ากับครึ่งหนึ่งของสัมประสิทธิ์ที่สอดคล้องกันของรูปแบบกำลังสอง นั่นเป็นเหตุผล
ปล่อยให้เมทริกซ์คอลัมน์ของตัวแปร X ได้รับโดยการแปลงเชิงเส้นที่ไม่เสื่อมของเมทริกซ์คอลัมน์ Y เช่น X = CY โดยที่ C คือเมทริกซ์ที่ไม่เอกพจน์ในลำดับที่ n จากนั้นรูปแบบกำลังสอง f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) =Y T (C T AC)Y
ดังนั้น ด้วยการแปลงเชิงเส้นที่ไม่เสื่อมลง C เมทริกซ์ของรูปแบบกำลังสองจึงมีรูปแบบ: A * =C T AC
ตัวอย่างเช่น ลองหารูปแบบกำลังสอง f(y 1, y 2) ซึ่งได้จากรูปแบบกำลังสอง f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 โดยการแปลงเชิงเส้น
รูปทรงกำลังสองเรียกว่า ตามบัญญัติ(มันมี มุมมองที่เป็นที่ยอมรับ) ถ้าสัมประสิทธิ์ทั้งหมดคือ ij = 0 สำหรับ i≠j นั่นคือ f(x 1, x 2,...,x n) = a 11 x 1 2 + a 22 x 2 2 + … + a nn x n 2 =
เมทริกซ์ของมันคือเส้นทแยงมุม
ทฤษฎีบท(ไม่ได้ให้หลักฐานไว้ที่นี่) รูปแบบกำลังสองใดๆ สามารถถูกลดให้เป็นรูปแบบมาตรฐานได้โดยใช้การแปลงเชิงเส้นที่ไม่เสื่อมลง
ตัวอย่างเช่น ลองนำรูปแบบมาตรฐานมาใช้ในรูปแบบกำลังสอง f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 – x 2 x 3
เมื่อต้องการทำสิ่งนี้ ขั้นแรกให้เลือกกำลังสองที่สมบูรณ์ด้วยตัวแปร x 1:
ฉ(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 – x 2 x 3 = 2(x 1 + x 2) 2 - 5x 2 2 – x 2 x 3
ตอนนี้เราเลือกกำลังสองที่สมบูรณ์ด้วยตัวแปร x 2:
ฉ(x 1, x 2, x 3) = 2(x 1 + x 2) 2 – 5(x 2 2 – 2* x 2 *(1/10)x 3 + (1/100)x 3 2) - (5/100)x 3 2 = = 2(x 1 + x 2) 2 – 5(x 2 – (1/10)x 3) 2 - (1/20)x 3 2.
จากนั้น การแปลงเชิงเส้นที่ไม่เสื่อมลง y 1 = x 1 + x 2,y 2 = x 2 – (1/10)x 3 และ y 3 = x 3 นำรูปแบบกำลังสองนี้มาสู่รูปแบบมาตรฐาน f(y 1,y 2, ปี 3) = 2ปี 1 2 - 5ปี 2 2 - (1/20)ปี 3 2 .
โปรดทราบว่ารูปแบบมาตรฐานของรูปแบบกำลังสองถูกกำหนดไว้อย่างคลุมเครือ (รูปแบบกำลังสองเดียวกันสามารถลดเป็นรูปแบบมาตรฐานได้ด้วยวิธีที่ต่างกัน 1) อย่างไรก็ตาม รูปแบบมาตรฐานที่ได้รับจากวิธีการต่างๆ มีคุณสมบัติทั่วไปหลายประการ โดยเฉพาะอย่างยิ่ง จำนวนพจน์ที่มีค่าสัมประสิทธิ์บวก (ลบ) ของรูปแบบกำลังสองไม่ได้ขึ้นอยู่กับวิธีการลดรูปแบบให้อยู่ในรูปแบบนี้ (ตัวอย่างเช่น ในตัวอย่างที่พิจารณาว่าจะมีค่าสัมประสิทธิ์ลบสองค่าและค่าบวกหนึ่งค่าเสมอ) คุณสมบัตินี้มีชื่อว่า กฎความเฉื่อยของรูปแบบกำลังสอง.
ขอให้เราตรวจสอบสิ่งนี้โดยนำรูปแบบกำลังสองเดียวกันมาสู่รูปแบบมาตรฐานในรูปแบบที่ต่างออกไป มาเริ่มการแปลงด้วยตัวแปร x 2:f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 – x 2 x 3 = -3x 2 2 – x 2 x 3 + 4x 1 x 2 + 2x 1 2 = -3(x 2 2 – - 2* x 2 ((1/6) x 3 + (2/3)x 1) +((1/6) x 3 + (2 /3) x 1) 2) – 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 = = -3(x 2 – (1/6) x 3 - (2 /3) x 1) 2 – 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 =f(y 1 ,y 2 ,y 3) = -3y 1 2 - - 3y 2 2 + 2y 3 2 โดยที่ y 1 = - (2/3)x 1 + x 2 – (1/6) x 3 ,y 2 = (2/3)x 1 + (1/6) x 3 และ y 3 = x 1 . ที่นี่มีค่าสัมประสิทธิ์บวกเป็น 2 สำหรับ y 3 และค่าสัมประสิทธิ์ลบสองตัว (-3) สำหรับ y 1 และ y 2 (และเมื่อใช้วิธีอื่น เราได้ค่าสัมประสิทธิ์บวกเป็น 2 สำหรับ y 1 และค่าลบสองตัว - (-5) สำหรับ y 2 และ (-1/20) สำหรับ y 3 )
ควรสังเกตด้วยว่าอันดับของเมทริกซ์รูปแบบกำลังสองเรียกว่า อันดับของรูปแบบกำลังสองเท่ากับจำนวนสัมประสิทธิ์ที่ไม่ใช่ศูนย์ของรูปแบบมาตรฐานและไม่เปลี่ยนแปลงภายใต้การแปลงเชิงเส้น
รูปแบบกำลังสอง f(X) เรียกว่า ในเชิงบวก(เชิงลบ)แน่ใจ, ถ้าค่าทั้งหมดของตัวแปรที่ไม่เป็นศูนย์พร้อมกันจะเป็นค่าบวก เช่น f(X) > 0 (ค่าลบ เช่น f(X)< 0).
ตัวอย่างเช่น รูปกำลังสอง f 1 (X) = x 1 2 + x 2 2 เป็นค่าแน่นอนที่เป็นบวก เนื่องจาก คือผลรวมของกำลังสอง และรูปแบบกำลังสอง f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 เป็นค่าจำกัดที่แน่นอน เนื่องจาก แสดงว่าสามารถแสดงได้ในรูปแบบ f 2 (X) = -(x 1 - x 2) 2.
ในสถานการณ์จริงส่วนใหญ่ การสร้างเครื่องหมายที่แน่นอนของรูปกำลังสองจะยากกว่า ดังนั้นในกรณีนี้เราใช้ทฤษฎีบทใดทฤษฎีหนึ่งต่อไปนี้ (เราจะกำหนดโดยไม่ต้องพิสูจน์)
ทฤษฎีบท. รูปแบบกำลังสองเป็นบวก (ลบ) แน่นอนหากค่าลักษณะเฉพาะทั้งหมดของเมทริกซ์เป็นบวก (ลบ)
ทฤษฎีบท (เกณฑ์ซิลเวสเตอร์). รูปแบบกำลังสองมีค่าเป็นบวกแน่นอนก็ต่อเมื่อค่ารองนำหน้าทั้งหมดของเมทริกซ์ในรูปแบบนี้เป็นบวกเท่านั้น
หลัก (มุม) ผู้เยาว์เมทริกซ์ลำดับที่ k ของลำดับที่ เรียกว่าดีเทอร์มิแนนต์ของเมทริกซ์ ซึ่งประกอบด้วย k แถวและคอลัมน์แรกของเมทริกซ์ A ()
โปรดทราบว่าสำหรับรูปกำลังสองแน่นอนที่เป็นลบ เครื่องหมายของตัวรองหลักจะสลับกัน และตัวรองอันดับแรกต้องเป็นค่าลบ
ตัวอย่างเช่น ลองตรวจสอบรูปแบบกำลังสอง f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 เพื่อดูความแน่นอนของเครื่องหมาย
= (2 -)* *(3 -) – 4 = (6 - 2- 3+ 2) – 4 = 2 - 5ï+ 2 = 0;D= 25 – 8 = 17; 
. ดังนั้นรูปกำลังสองจึงเป็นค่าแน่นอนที่เป็นบวก
วิธีที่ 2 Principal minor ของลำดับแรกของเมทริกซ์ A 1 =a 11 = 2 > 0 Principal minor ของลำดับที่สอง 2 = = 6 – 4 = 2 > 0 ดังนั้น ตามเกณฑ์ของ Sylvester ค่ากำลังสอง ฟอร์มเป็นบวกแน่นอน
เราตรวจสอบรูปแบบกำลังสองอีกรูปแบบหนึ่งเพื่อหาค่าแน่นอนของเครื่องหมาย f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2
วิธีที่ 1 มาสร้างเมทริกซ์กำลังสองรูปแบบ A = กันดีกว่า สมการคุณลักษณะจะมีรูปแบบ 
= (-2 -ïL)* *(-3 -ïL) – 4 = (6 + 2+ 3+ï 2) – 4 = 2 + 5ï+ 2 = 0;D= 25 – 8 = 17 ; 
. ดังนั้นรูปกำลังสองจึงเป็นค่าแน่นอนเชิงลบ
วิธีที่ 2 หลักของลำดับแรกของเมทริกซ์ A 1 =a 11 = = -2< 0. Главный минор второго порядка 2 = = 6 – 4 = 2 >0. ดังนั้น ตามเกณฑ์ของซิลเวสเตอร์ รูปแบบกำลังสองจึงเป็นค่าแน่นอนที่เป็นลบ (เครื่องหมายของผู้เยาว์หลักสลับกัน โดยเริ่มจากเครื่องหมายลบ)
และอีกตัวอย่างหนึ่ง เราจะตรวจสอบรูปแบบกำลังสองที่กำหนดเครื่องหมาย f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2
วิธีที่ 1 มาสร้างเมทริกซ์กำลังสองรูปแบบ A = กันดีกว่า สมการคุณลักษณะจะมีรูปแบบ 
= (2 -ï)* *(-3 -ïL) – 4 = (-6 - 2ïL+ 3`+ï 2) – 4 =` 2 +`- 10 = 0;D= 1 + 40 = 41; 
. หนึ่งในจำนวนเหล่านี้เป็นลบและอีกจำนวนหนึ่งเป็นค่าบวก สัญญาณของค่าลักษณะเฉพาะนั้นแตกต่างกัน ดังนั้น รูปกำลังสองจึงไม่สามารถกำหนดนิยามทั้งทางลบและทางบวกได้ กล่าวคือ รูปแบบกำลังสองนี้ไม่มีเครื่องหมายที่แน่นอน (สามารถรับค่าของเครื่องหมายใดก็ได้)
วิธีที่ 2. หลักรองของลำดับแรกของเมทริกซ์ A 1 =a 11 = 2 > 0. หลักรองของลำดับที่สอง 2 = = -6 – 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них – положителен).
1วิธีที่พิจารณาในการลดรูปแบบกำลังสองเป็นรูปแบบมาตรฐานนั้นสะดวกต่อการใช้งานเมื่อพบค่าสัมประสิทธิ์ที่ไม่เป็นศูนย์กับกำลังสองของตัวแปร หากไม่มีอยู่ ก็ยังสามารถดำเนินการแปลงได้ แต่คุณต้องใช้เทคนิคอื่น ตัวอย่างเช่น ให้ f(x 1, x 2) = 2x 1 x 2 = x 1 2 + 2x 1 x 2 + x 2 2 - x 1 2 - x 2 2 =
= (x 1 + x 2) 2 - x 1 2 - x 2 2 = (x 1 + x 2) 2 – (x 1 2 - 2x 1 x 2 + x 2 2) - 2x 1 x 2 = (x 1 + x 2) 2 – - (x 1 - x 2) 2 - 2x 1 x 2 ; 4x 1 x 2 = (x 1 + x 2) 2 – (x 1 - x 2) 2 ;f(x 1, x 2) = 2x 1 x 2 = (1/2)* *(x 1 + x 2 ) 2 – (1/2)*(x 1 - x 2) 2 =f(y 1 ,y 2) = (1/2)y 1 2 – (1/2)y 2 2 โดยที่ y 1 = x 1 + x 2 หรือ 2 = x 1 – x 2
พหุนามเอกพันธ์ระดับ 2 ในหลายตัวแปรเรียกว่ารูปแบบกำลังสอง
ตัวแปรรูปแบบกำลังสองประกอบด้วยเงื่อนไขสองประเภท: ตัวแปรกำลังสองและผลคูณคู่ของตัวแปรที่มีค่าสัมประสิทธิ์ที่แน่นอน รูปแบบกำลังสองมักจะเขียนเป็นแผนภาพสี่เหลี่ยมต่อไปนี้:
คู่คำศัพท์ที่คล้ายกันเขียนด้วยค่าสัมประสิทธิ์เท่ากัน เพื่อให้แต่ละคำประกอบด้วยครึ่งหนึ่งของค่าสัมประสิทธิ์ของผลิตภัณฑ์ที่สอดคล้องกันของตัวแปร ดังนั้น รูปกำลังสองแต่ละรูปจึงสัมพันธ์กับเมทริกซ์สัมประสิทธิ์ซึ่งเป็นสมมาตรโดยธรรมชาติ
สะดวกในการแสดงรูปแบบกำลังสองในรูปแบบเมทริกซ์ต่อไปนี้ ให้เราแสดงด้วย X คอลัมน์ของตัวแปรผ่าน X - แถวนั่นคือเมทริกซ์ที่ย้ายด้วย X แล้วก็
แบบฟอร์มกำลังสองพบได้ในคณิตศาสตร์หลายแขนงและการประยุกต์
ในทฤษฎีจำนวนและผลึกศาสตร์ รูปแบบกำลังสองได้รับการพิจารณาภายใต้สมมติฐานที่ว่าตัวแปรจะใช้เฉพาะค่าจำนวนเต็มเท่านั้น ในเรขาคณิตวิเคราะห์ รูปแบบกำลังสองเป็นส่วนหนึ่งของสมการของเส้นโค้ง (หรือพื้นผิว) ของลำดับ ในกลศาสตร์และฟิสิกส์ รูปกำลังสองดูเหมือนจะแสดงพลังงานจลน์ของระบบผ่านส่วนประกอบของความเร็วทั่วไป ฯลฯ แต่นอกจากนี้ การศึกษารูปกำลังสองยังจำเป็นในการวิเคราะห์เมื่อศึกษาฟังก์ชันของตัวแปรหลายตัวในคำถาม ซึ่งเป็นสิ่งสำคัญที่จะต้องค้นหาว่าฟังก์ชันนี้ในบริเวณใกล้เคียงของจุดที่กำหนดเบี่ยงเบนไปจากฟังก์ชันเชิงเส้นที่ประมาณค่าได้อย่างไร ตัวอย่างของปัญหาประเภทนี้คือการศึกษาฟังก์ชันเพื่อหาค่าสูงสุดและค่าต่ำสุด
ตัวอย่างเช่น ลองพิจารณาปัญหาในการศึกษาค่าสูงสุดและค่าต่ำสุดของฟังก์ชันของตัวแปรสองตัวที่มีอนุพันธ์ย่อยต่อเนื่องกันตามลำดับ เงื่อนไขที่จำเป็นสำหรับจุดที่จะให้ค่าสูงสุดหรือต่ำสุดของฟังก์ชันคืออนุพันธ์ย่อยของลำดับที่จุดนั้นเท่ากับศูนย์ ให้เราถือว่าเป็นไปตามเงื่อนไขนี้ ลองให้ตัวแปร x และ y เพิ่มขึ้นเล็กน้อยและ k แล้วพิจารณาการเพิ่มขึ้นของฟังก์ชันที่สอดคล้องกัน ตามสูตรของ Taylor การเพิ่มขึ้นนี้จนถึงลำดับที่สูงกว่าเล็กน้อยจะเท่ากับรูปแบบกำลังสองโดยที่ค่าของอนุพันธ์อันดับสองคือ คำนวณ ณ จุด หากรูปแบบกำลังสองนี้เป็นบวกสำหรับค่าทั้งหมดของ และ k (ยกเว้น ) ฟังก์ชันจะมีค่าต่ำสุดที่จุด หากเป็นลบ ก็จะมีค่าสูงสุด สุดท้ายนี้ หากแบบฟอร์มใช้ทั้งค่าบวกและค่าลบ ก็จะไม่มีค่าสูงสุดหรือค่าต่ำสุด ฟังก์ชันของตัวแปรจำนวนมากก็ได้รับการศึกษาในลักษณะเดียวกันเช่นกัน
การศึกษารูปแบบกำลังสองส่วนใหญ่ประกอบด้วยการศึกษาปัญหาความเท่าเทียมกันของรูปแบบที่เกี่ยวข้องกับการแปลงเชิงเส้นชุดหนึ่งหรือหลายชุดของตัวแปร กล่าวกันว่ารูปแบบกำลังสองสองรูปแบบจะเท่ากันหากหนึ่งในนั้นสามารถแปลงเป็นอีกรูปแบบหนึ่งได้โดยการแปลงอย่างใดอย่างหนึ่งของเซตที่กำหนด ที่เกี่ยวข้องอย่างใกล้ชิดกับปัญหาความเท่าเทียมกันคือปัญหาในการลดรูปแบบเช่น เปลี่ยนมันให้เป็นรูปแบบที่ง่ายที่สุด
ในคำถามต่างๆ ที่เกี่ยวข้องกับรูปแบบกำลังสอง จะมีการพิจารณาชุดการแปลงตัวแปรที่ยอมรับได้หลายชุดด้วย
ในคำถามของการวิเคราะห์ จะใช้การแปลงตัวแปรที่ไม่พิเศษใดๆ สำหรับวัตถุประสงค์ของเรขาคณิตเชิงวิเคราะห์ การแปลงมุมฉากเป็นที่สนใจมากที่สุด กล่าวคือ การแปลงที่สอดคล้องกับการเปลี่ยนจากระบบพิกัดคาร์ทีเซียนแบบแปรผันหนึ่งไปยังอีกระบบหนึ่ง ในที่สุด ในทฤษฎีจำนวนและการแปลงเชิงเส้นของผลึกศาสตร์ด้วยค่าสัมประสิทธิ์จำนวนเต็มและมีปัจจัยกำหนดเท่ากับความสามัคคีจะถูกพิจารณา
เราจะพิจารณาปัญหาสองประการนี้: คำถามเรื่องการลดรูปแบบกำลังสองให้เหลือรูปแบบที่ง่ายที่สุดผ่านการแปลงที่ไม่ใช่เอกพจน์ และคำถามเดียวกันสำหรับการแปลงมุมตั้งฉาก ก่อนอื่น เรามาดูกันว่าเมทริกซ์รูปกำลังสองถูกแปลงอย่างไรระหว่างการแปลงตัวแปรเชิงเส้น
อนุญาต โดยที่ A คือเมทริกซ์สมมาตรของค่าสัมประสิทธิ์รูปแบบ X คือคอลัมน์ของตัวแปร
เรามาสร้างการแปลงเชิงเส้นของตัวแปรกัน โดยเขียนย่อว่า . โดยที่ C หมายถึงเมทริกซ์ของสัมประสิทธิ์ของการแปลงนี้ X คือคอลัมน์ของตัวแปรใหม่ จากนั้นและด้วยเหตุนี้ ดังนั้น เมทริกซ์ของรูปกำลังสองที่ถูกเปลี่ยนรูปจึงเป็นเช่นนี้
เมทริกซ์จะกลายเป็นสมมาตรโดยอัตโนมัติ ซึ่งง่ายต่อการตรวจสอบ ดังนั้น ปัญหาในการลดรูปแบบกำลังสองให้อยู่ในรูปแบบที่ง่ายที่สุดจึงเทียบเท่ากับปัญหาในการลดเมทริกซ์สมมาตรให้อยู่ในรูปแบบที่ง่ายที่สุดโดยการคูณเมทริกซ์ทางซ้ายและขวาด้วยเมทริกซ์ที่ย้ายซึ่งกันและกัน
