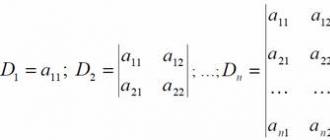Правила за въвеждане на функции:
Два пъти непрекъснато диференцируема функция f(x) е изпъкнала (вдлъбната) тогава и само ако Хесианова матрицафункцията f(x) по отношение на x е положителна (отрицателна) полуопределена за всички x (виж точките на локални екстремуми на функция на няколко променливи).
Функционални критични точки:
- ако хесианът е положително определен, тогава x 0 е локалната минимална точка на функцията f(x),
- ако Хесианът е отрицателно определен, тогава x 0 е локалната максимална точка на функцията f(x),
- ако хесианът не е знакоопределен (приема както положителни, така и отрицателни стойности) и не е изроден (det G(f) ≠ 0), тогава x 0 е седловата точка на функцията f(x).
Критерии за определеност на матрица (теорема на Силвестър)
Положителна сигурност:- всички диагонални елементи на матрицата трябва да са положителни;
- всички водещи главни квалификации трябва да са положителни.
Положителна полуопределеност:
- всички диагонални елементи са неотрицателни;
- всички основни детерминанти са неотрицателни.
Квадратна симетрична матрица от ред n, чиито елементи са частни производни на целевата функция от втори ред, наречена матрица на Хесиани се обозначава:
За да бъде една симетрична матрица положително определена, е необходимо и достатъчно всички нейни диагонални минори да са положителни, т.е. 
за матрицата A = (a ij) са положителни.
Отрицателна сигурност.
За да бъде една симетрична матрица отрицателно определена, е необходимо и достатъчно да са изпълнени следните неравенства:
(-1) k D k > 0, к=1,.., n.
С други думи, за да бъде квадратичната форма отрицателно определено, е необходимо и достатъчно знаците на ъгловите минори на матрица с квадратична форма да се редуват, започвайки със знака минус. Например, за две променливи, D 1< 0, D 2 > 0.
Ако Хесианът е полуопределен, тогава това също може да е инфлексна точка. Необходими са допълнителни изследвания, които могат да се извършат по един от следните варианти:
- Намаляващ ред. Извършва се промяна на променливите. Например, за функция на две променливи е y=x, като резултат получаваме функция на една променлива x. След това изследваме поведението на функцията на линиите y=x и y=-x. Ако в първия случай функцията в изследваната точка ще има минимум, а в другия случай максимум (или обратното), тогава изследваната точка е седлова точка.
- Намиране на собствените стойности на Хесиан. Ако всички стойности са положителни, функцията в изследваната точка има минимум, ако всички стойности са отрицателни, има максимум.
- Изследване на функцията f(x) в околността на точка ε. Променливите x се заменят с x 0 +ε. След това е необходимо да се докаже, че функцията f(x 0 +ε) на една променлива ε е или по-голяма от нула (тогава x 0 е минималната точка) или по-малка от нула (тогава x 0 е максималната точка).
Забележка. Да намеря обратен хесиандостатъчно е да се намери обратната матрица.
Пример №1. Кои от следните функции са изпъкнали или вдлъбнати: f(x) = 8x 1 2 +4x 1 x 2 +5x 2 2 .
Решение. 1. Да намерим частни производни. 
2. Да решим системата от уравнения.
-4x 1 +4x 2 +2 = 0
4x 1 -6x 2 +6 = 0
Получаваме:
а) От първото уравнение изразяваме x 1 и го заместваме във второто уравнение:
x 2 = x 2 + 1/2
-2x 2 +8 = 0
Където x 2 = 4
Ние заместваме тези стойности x 2 в израза за x 1. Получаваме: x 1 = 9 / 2
Броят на критичните точки е 1.
М 1 (9 / 2 ;4)
3. Да намерим частните производни от втори ред.
4. Нека изчислим стойността на тези частни производни от втори ред в критичните точки M(x 0 ; y 0).
Изчисляваме стойностите за точка M 1 (9 / 2; 4) 
Изграждаме матрицата на Хесиан:
D 1 = a 11< 0, D 2 = 8 > 0
Тъй като диагоналните минори имат различни знаци, нищо не може да се каже за изпъкналостта или вдлъбнатостта на функцията.
Въведение…………………………………………………………….......................... ......... .................3
1 Теоретична информация за квадратичните форми……………………………4
1.1 Дефиниция на квадратна форма……………………………………….…4
1.2 Намаляване на квадратична форма до канонична форма ……………… ... 6
1.3 Закон за инерцията…………………………………………………………….….11
1.4 Положителни определени форми……………………………………...18
2 Практическо приложение на квадратни форми …………………………22
2.1 Решаване на типични проблеми………………………………………………………………22
2.2 Задачи за самостоятелно решаване………………………….………...26
2.3 Тестови задачи…………………………………………………………………...27
Заключение………………………………………………………………………29
Списък на използваната литература……………………………………………………...30
ВЪВЕДЕНИЕ
Първоначално теорията на квадратичните форми се използва за изследване на криви и повърхности, дефинирани от уравнения от втори ред, съдържащи две или три променливи. По-късно тази теория намира други приложения. По-специално, при математическо моделиране на икономически процеси, целевите функции могат да съдържат квадратични членове. Многобройни приложения на квадратни форми изискват изграждането на обща теория, когато броят на променливите е равен на всяка
, а коефициентите на квадратичната форма не винаги са реални числа.Теорията на квадратичните форми е разработена за първи път от френския математик Лагранж, който притежава много идеи в тази теория; по-специално той въвежда важната концепция за намалена форма, с помощта на която доказва крайността на броя на класовете на двоични квадратични форми на даден дискриминант. След това тази теория беше значително разширена от Гаус, който въведе много нови концепции, въз основа на които той успя да получи доказателства за трудни и дълбоки теореми на теорията на числата, които убягваха на неговите предшественици в тази област.
Целта на работата е да се изучат видовете квадратични форми и начините за намаляване на квадратичните форми до канонична форма.
Тази работа поставя следните задачи: подбор на необходимата литература, разглеждане на определения, решаване на редица проблеми и подготовка на тестове.
1 ТЕОРЕТИЧНА ИНФОРМАЦИЯ ЗА КВАДРАТИЧНИТЕ ФОРМИ
1.1 ДЕФИНИЦИЯ НА КВАДРАТИЧНА ФОРМА
Квадратна форма
на неизвестни е сбор, всеки член от който е или квадрат на едно от тези неизвестни, или продукт на две различни неизвестни. Квадратната форма се предлага в две форми: реална и комплексна, в зависимост от това дали нейните коефициенти са реални или комплексни числа.Означавайки коефициента при
през , и при производство
, през 
, квадратната форма може да бъде представена като: . От коефициентите
възможно е да се построи квадратна матрица от ред ; тя се нарича матрица на квадратична форма, а нейният ранг се нарича ранг на квадратичната форма. Ако, по-специално, , където , тоест матрицата е недегенерирана, тогава квадратичната форма се нарича недегенерирана. За всяка симетрична матрица от ред може да се определи в напълно дефинирана квадратна форма:
(1.1) - неизвестни, имащи матрични елементи с техните коефициенти. Нека сега обозначим с
колона, съставена от неизвестни: . е матрица с редове и една колона. Транспонирайки тази матрица, получаваме матрицата:
, съставен от един ред. Квадратична форма (1.1) с матрица
вече може да се запише като продукт:.1.2 ПРИВЕДЕНИЕ ДО КВАДРАТИЧНА ФОРМА
КЪМ КАНОНИЧНИЯ ГЛЕД
Да предположим, че квадратната форма
от неизвестните вече е намален чрез неизродена линейна трансформация до каноничната форма, където са новите неизвестни. Някои от коефициентите може да са нула. Нека докажем, че броят на ненулевите коефициенти е задължително равен на ранга на формата. Матрицата на тази квадратна форма има диагонална форма
,
и изискването тази матрица да има ранг
, е еквивалентно на предположението, че главният му диагонал съдържа точно ненулеви елементи.Теорема.Всяка квадратична форма може да бъде редуцирана до канонична форма чрез някакво неизродено линейно преобразуване. Ако се разглежда реална квадратна форма, тогава всички коефициенти на посочената линейна трансформация могат да се считат за реални.
Доказателство. Тази теорема е вярна за случая на квадратни форми с едно неизвестно, тъй като всяка такава форма има формата
, което е канонично. Нека въведем доказателство чрез индукция, тоест да докажем теоремата за квадратни форми с неизвестни, като се има предвид, че тя вече е доказана за форми с по-малък брой неизвестни.Нека квадратичната форма (1.1) на
При решаването на различни приложни задачи често е необходимо да се изучават квадратни форми.
Определение.Квадратна форма L(, x 2, ..., x n) на n променливи е сбор, всеки член от който е или квадрат на една от променливите, или произведение на две различни променливи, взети с определен коефициент:
L( ,x 2 ,...,x n) =
Предполагаме, че коефициентите на квадратичната форма са реални числа и
Матрицата A = () (i, j = 1, 2, ..., n), съставена от тези коефициенти, се нарича матрица с квадратична форма.
В матричната нотация квадратната форма има формата: L = X"AX, където X = (x 1, x 2,..., x n)" - матрица-колона от променливи.
Пример 8.1
Напишете квадратната форма L( , x 2 , x 3) = в матрична форма.
Нека намерим матрица с квадратна форма. Диагоналните му елементи са равни на коефициентите на квадратите на променливите, т.е. 4, 1, -3, а други елементи - към половините на съответните коефициенти на квадратната форма. Ето защо
L=( , x 2 , x 3) 
.
С недегенерирана линейна трансформация X = CY, матрицата на квадратната форма приема формата: A * = C "AC. (*)
Пример 8.2
Дадена е квадратичната форма L(x x, x 2) =2x 1 2 +4x 1 x 2 -3. Намерете квадратичната форма L(y 1 ,y 2), получена от дадената линейна трансформация = 2у 1 - 3y 2 , x 2 = y 1 + y 2.
Матрицата на дадена квадратна форма е A= , а матрицата на линейната трансформация е
C = . Следователно, според (*) матрица на търсената квадратна форма
И квадратната форма изглежда така
L(y 1, y 2) =
.
Трябва да се отбележи, че с някои добре подбрани линейни трансформации формата на квадратната форма може значително да се опрости.
Определение.Квадратната форма L(,x 2,...,x n) = се нарича канонична (или има канонична форма), ако всички нейни коефициенти = 0 за i¹j:
L= 
, а матрицата му е диагонална.
Следната теорема е вярна.
Теорема.Всяка квадратична форма може да бъде редуцирана до канонична форма с помощта на неизродена линейна трансформация на променливи.
Пример 8.3
Редуцирайте квадратичната форма до канонична форма
L( , x 2 , x 3) =
Първо избираме пълния квадрат на променливата, чийто коефициент на квадрат е различен от нула:
Сега избираме идеалния квадрат за променливата, чийто коефициент е различен от нула:
И така, неизродена линейна трансформация
намалява тази квадратна форма до канонична форма: 
Каноничната форма на квадратична форма не е еднозначно дефинирана, тъй като същата квадратна форма може да бъде намалена до каноничната форма по много начини. Въпреки това, каноничните форми, получени по различни методи, имат редица общи свойства. Нека формулираме едно от тези свойства като теорема.
Теорема (закон за инерцията на квадратичните форми).Броят на членовете с положителни (отрицателни) коефициенти на квадратичната форма не зависи от метода за редуциране на формата до тази форма.
Трябва да се отбележи, че рангът на матрица на квадратна форма е равен на броя на ненулевите коефициенти на каноничната форма и не се променя при линейни трансформации.
Определение.Квадратната форма L(, x 2, ..., x n) се нарича положителна (отрицателна) определена, ако за всички стойности на променливите, поне една от които е различна от нула,
L( , x 2 , ..., x n) > 0 (L( , x 2 , ..., x n)< 0).
Така, Например, квадратна форма 
е положително определена, а формата е отрицателно определена.
Теорема.За да бъде квадратичната форма L = X"AX положителна (отрицателна) определена, е необходимо и достатъчно всички собствени стойности на матрица A да са положителни (отрицателни).
Квадратна форма f(x 1, x 2,...,x n) от n променливи е сбор, всеки член от който е или квадрат на една от променливите, или произведение на две различни променливи, взети с определен коефициент: f (x 1, x 2, ...,x n) = (a ij =a ji).
Матрицата А, съставена от тези коефициенти, се нарича матрица с квадратична форма. Винаги е така симетриченматрица (т.е. матрица, симетрична спрямо главния диагонал, a ij =a ji).
В матричната нотация квадратичната форма е f(X) = X T AX, където
Наистина
Например, нека запишем квадратната форма в матрична форма.
За да направим това, намираме матрица с квадратна форма. Нейните диагонални елементи са равни на коефициентите на квадратните променливи, а останалите елементи са равни на половинките на съответните коефициенти на квадратната форма. Ето защо
Нека колоната на матрицата от променливи X се получава чрез неизродена линейна трансформация на колоната на матрицата Y, т.е. X = CY, където C е неособена матрица от n-ти ред. Тогава квадратичната форма f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) =Y T (C T AC)Y.
По този начин, с недегенерирана линейна трансформация C, матрицата на квадратна форма приема формата: A * =C T AC.
Например, нека намерим квадратичната форма f(y 1, y 2), получена от квадратичната форма f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 чрез линейна трансформация.
Квадратната форма се нарича каноничен(То има каноничен изглед), ако всички негови коефициенти a ij = 0 за i≠j, т.е. f(x 1, x 2,...,x n) = a 11 x 1 2 + a 22 x 2 2 + … + a nn x n 2 = .
Матрицата му е диагонална.
Теорема(доказателството не е дадено тук). Всяка квадратна форма може да бъде редуцирана до канонична форма с помощта на неизродена линейна трансформация.
Например, нека приведем в канонична форма квадратичната форма f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 – x 2 x 3.
За да направите това, първо изберете пълен квадрат с променливата x 1:
f(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 – x 2 x 3 = 2(x 1 + x 2) 2 - 5x 2 2 – x 2 x 3.
Сега избираме пълен квадрат с променливата x 2:
f(x 1, x 2, x 3) = 2(x 1 + x 2) 2 – 5(x 2 2 – 2* x 2 *(1/10)x 3 + (1/100)x 3 2) - (5/100)x 3 2 = = 2(x 1 + x 2) 2 – 5(x 2 – (1/10)x 3) 2 - (1/20)x 3 2.
Тогава неизродената линейна трансформация y 1 = x 1 + x 2,y 2 = x 2 – (1/10)x 3 и y 3 = x 3 довежда тази квадратна форма до каноничната форма f(y 1,y 2, y 3) = 2y 1 2 - 5y 2 2 - (1/20)y 3 2 .
Обърнете внимание, че каноничната форма на квадратична форма се определя нееднозначно (една и съща квадратна форма може да бъде редуцирана до канонична форма по различни начини 1). Въпреки това, каноничните форми, получени по различни методи, имат редица общи свойства. По-специално, броят на термините с положителни (отрицателни) коефициенти на квадратична форма не зависи от метода за редуциране на формата до тази форма (например в разглеждания пример винаги ще има два отрицателни и един положителен коефициент). Това свойство се нарича закон за инерцията на квадратичните форми.
Нека проверим това, като приведем същата квадратна форма в канонична форма по различен начин. Нека започнем трансформацията с променливата x 2:f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 – x 2 x 3 = -3x 2 2 – x 2 x 3 + 4x 1 x 2 + 2x 1 2 = -3(x 2 2 – - 2* x 2 ((1/6) x 3 + (2/3)x 1) +((1/6) x 3 + (2) /3) x 1) 2) – 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 = = -3(x 2 – (1/6) x 3 - (2) /3) x 1) 2 – 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 =f(y 1,y 2,y 3) = -3y 1 2 - - 3y 2 2 + 2y 3 2, където y 1 = - (2/3)x 1 + x 2 – (1/6) x 3, y 2 = (2/3)x 1 + (1/6) x 3 и y 3 = x 1 . Тук има положителен коефициент 2 за y 3 и два отрицателни коефициента (-3) за y 1 и y 2 (и използвайки друг метод, получихме положителен коефициент 2 за y 1 и два отрицателни - (-5) за y 2 и (-1/20) за y 3 ).
Трябва също да се отбележи, че рангът на матрица с квадратична форма, т.нар ранг на квадратна форма, е равен на броя на ненулевите коефициенти на каноничната форма и не се променя при линейни трансформации.
Квадратната форма f(X) се нарича положително(отрицателен)определени, ако за всички стойности на променливите, които не са едновременно нула, той е положителен, т.е. f(X) > 0 (отрицателен, т.е. f(X)< 0).
Например, квадратичната форма f 1 (X) = x 1 2 + x 2 2 е положително определена, тъй като е сбор от квадрати, а квадратната форма f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 е отрицателно определена, тъй като представлява може да бъде представено във формата f 2 (X) = -(x 1 - x 2) 2.
В повечето практически ситуации е малко по-трудно да се установи определен знак на квадратна форма, така че за това използваме една от следните теореми (ще ги формулираме без доказателство).
Теорема. Квадратната форма е положителна (отрицателна) определена тогава и само ако всички собствени стойности на нейната матрица са положителни (отрицателни).
Теорема (критерий на Силвестър). Квадратната форма е положително определена тогава и само ако всички водещи минори на матрицата на тази форма са положителни.
Основен (ъглов) минорМатриците от k-ти ред от An-ти ред се наричат детерминанта на матрицата, съставена от първите k реда и колони на матрицата A ().
Забележете, че за отрицателно определени квадратни форми знаците на главните минори се редуват и минорът от първи ред трябва да е отрицателен.
Например, нека разгледаме квадратичната форма f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 за определеност на знака.
= (2 -)* *(3 -) – 4 = (6 - 2- 3+ 2) – 4 = 2 - 5+ 2 = 0; D= 25 – 8 = 17; 
. Следователно квадратната форма е положително определена.
Метод 2. Главен минор от първи ред на матрицата A 1 =a 11 = 2 > 0. Главен минор от втори ред 2 = = 6 – 4 = 2 > 0. Следователно, според критерия на Силвестър, квадратичната формата е положително определена.
Разглеждаме друга квадратна форма за определеност на знака, f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.
Метод 1. Нека изградим матрица с квадратична форма A = . Характеристичното уравнение ще има формата 
= (-2 -)* *(-3 -) – 4 = (6 + 2+ 3+ 2) – 4 = 2 + 5+ 2 = 0; D= 25 – 8 = 17 ; 
. Следователно квадратната форма е отрицателно определена.
Метод 2. Главен минор от първи ред на матрицата A 1 =a 11 = = -2< 0. Главный минор второго порядка 2 = = 6 – 4 = 2 >0. Следователно, според критерия на Силвестър, квадратичната форма е отрицателно определена (знаците на главните малки се редуват, започвайки с минуса).
И като друг пример, разглеждаме определената със знак квадратна форма f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2.
Метод 1. Нека изградим матрица с квадратична форма A = . Характеристичното уравнение ще има формата 
= (2 -)* *(-3 -) – 4 = (-6 - 2+ 3+ 2) – 4 = 2 +- 10 = 0; D= 1 + 40 = 41; 
. Едно от тези числа е отрицателно, а другото е положително. Знаците на собствените стойности са различни. Следователно квадратната форма не може да бъде нито отрицателно, нито положително определена, т.е. тази квадратична форма не е знакоопределена (може да приема стойности на всеки знак).
Метод 2. Главен минор от първи ред на матрица A 1 =a 11 = 2 > 0. Главен минор от втори ред 2 = = -6 – 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них – положителен).
1Разглежданият метод за редуциране на квадратична форма до канонична форма е удобен за използване, когато се срещат ненулеви коефициенти с квадратите на променливите. Ако те не са там, все още е възможно да се извърши преобразуването, но трябва да използвате някои други техники. Например, нека f(x 1, x 2) = 2x 1 x 2 = x 1 2 + 2x 1 x 2 + x 2 2 - x 1 2 - x 2 2 =
= (x 1 + x 2) 2 - x 1 2 - x 2 2 = (x 1 + x 2) 2 – (x 1 2 - 2x 1 x 2 + x 2 2) - 2x 1 x 2 = (x 1 + x 2) 2 – - (x 1 - x 2) 2 - 2x 1 x 2 ; 4x 1 x 2 = (x 1 + x 2) 2 – (x 1 - x 2) 2 ;f(x 1, x 2) = 2x 1 x 2 = (1/2)* *(x 1 + x 2) ) 2 – (1/2)*(x 1 - x 2) 2 =f(y 1 ,y 2) = (1/2)y 1 2 – (1/2)y 2 2, където y 1 = x 1 + x 2, аy 2 = x 1 – x 2.
Хомогенен полином от степен 2 на няколко променливи се нарича квадратна форма.
Квадратната форма на променливите се състои от членове от два вида: квадрати на променливи и техните произведения по двойки с определени коефициенти. Квадратната форма обикновено се записва като следната квадратна диаграма:
Двойките подобни членове се записват с равни коефициенти, така че всеки от тях да съставлява половината от коефициента на съответното произведение на променливите. По този начин всяка квадратна форма е естествено свързана със своята матрица на коефициента, която е симетрична.
Удобно е да се представи квадратната форма в следната матрична нотация. Нека обозначим с X колона от променливи през X - ред, т.е. матрица, транспонирана с X. Тогава
Квадратните форми се срещат в много клонове на математиката и нейните приложения.
В теорията на числата и кристалографията квадратичните форми се разглеждат при допускането, че променливите приемат само цели числа. В аналитичната геометрия квадратната форма е част от уравнението на крива (или повърхност) от ред. В механиката и физиката изглежда, че квадратичната форма изразява кинетичната енергия на система чрез компонентите на обобщените скорости и т.н. Но освен това изучаването на квадратичните форми е необходимо и при анализа, когато се изучават функции на много променливи, при въпроси за което е важно да се установи как тази функция в околността на дадена точка се отклонява от линейната функция, която я апроксимира. Пример за задача от този тип е изследването на функция за нейния максимум и минимум.
Помислете, например, за проблема за изследване на максимума и минимума за функция на две променливи, която има непрекъснати частни производни до ред. Необходимо условие точката да даде максимум или минимум на функция е частните производни на реда в точката да са равни на нула.Нека приемем, че това условие е изпълнено. Нека дадем малки увеличения на променливите x и y и k и да разгледаме съответното нарастване на функцията.Според формулата на Тейлър, това увеличение, до малки по-високи разряди, е равно на квадратната форма, където са стойностите на вторите производни изчислена в точка Ако тази квадратна форма е положителна за всички стойности на и k (с изключение на), тогава функцията има минимум в точката; ако е отрицателна, тогава има максимум. И накрая, ако една форма приема както положителни, така и отрицателни стойности, тогава няма да има максимум или минимум. Функциите на по-голям брой променливи също се изучават по подобен начин.
Изследването на квадратичните форми се състои главно от изучаване на проблема за еквивалентността на формите по отношение на един или друг набор от линейни трансформации на променливи. Две квадратни форми се наричат еквивалентни, ако едната от тях може да бъде преобразувана в другата чрез едно от преобразуванията на дадено множество. В тясна връзка с проблема за еквивалентността е проблемът за намаляване на формата, т.е. трансформирайки го в някаква възможно най-проста форма.
В различни въпроси, свързани с квадратични форми, също се разглеждат различни набори от допустими трансформации на променливи.
По въпросите на анализа се използват всякакви неспециални трансформации на променливи; за целите на аналитичната геометрия най-голям интерес представляват ортогоналните трансформации, т.е. тези, които съответстват на прехода от една система от променливи декартови координати към друга. И накрая, в теорията на числата и кристалографията се разглеждат линейни трансформации с цели коефициенти и детерминанта, равна на единица.
Ще разгледаме два от тези проблеми: въпросът за редуциране на квадратична форма до нейната най-проста форма чрез всякакви неособени трансформации и същия въпрос за ортогонални трансформации. Първо, нека разберем как се трансформира матрица с квадратична форма по време на линейна трансформация на променливи.
Нека , където A е симетрична матрица от коефициенти на формата, X е колона от променливи.
Нека направим линейна трансформация на променливи, записвайки я съкратено като . Тук C означава матрицата на коефициентите на тази трансформация, X е колона от нови променливи. Тогава и следователно матрицата на трансформираната квадратна форма е такава
Матрицата автоматично се оказва симетрична, което лесно се проверява. По този начин проблемът за редуциране на квадратна форма до най-простата форма е еквивалентен на проблема за редуциране на симетрична матрица до най-простата форма чрез умножаването й отляво и отдясно на взаимно транспонирани матрици.
